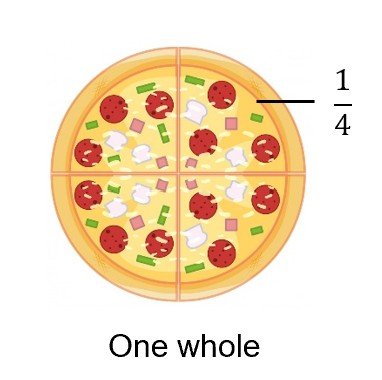
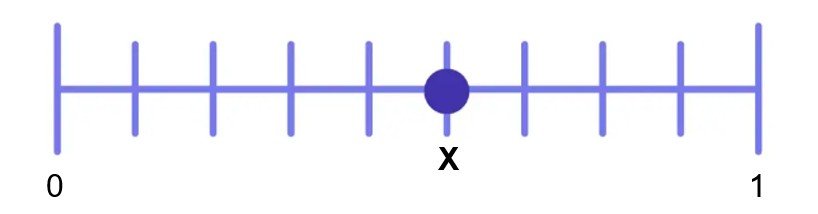
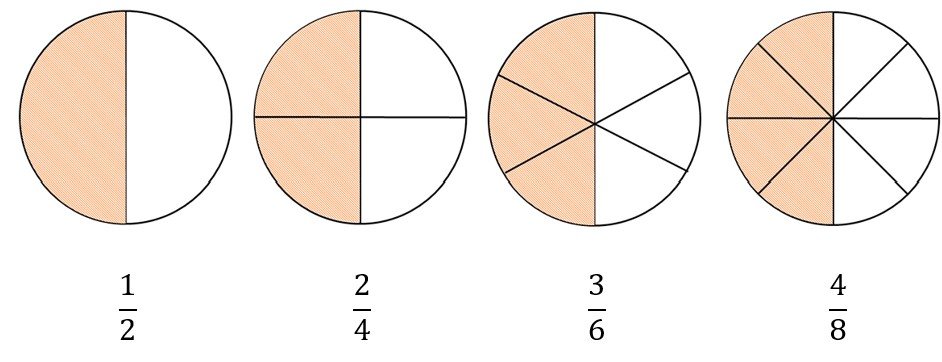
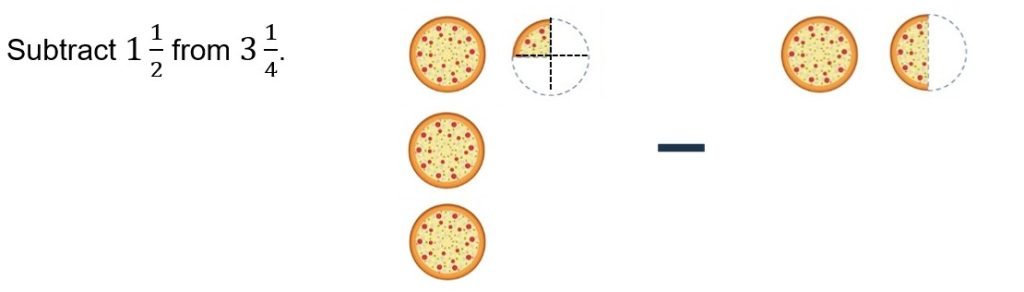
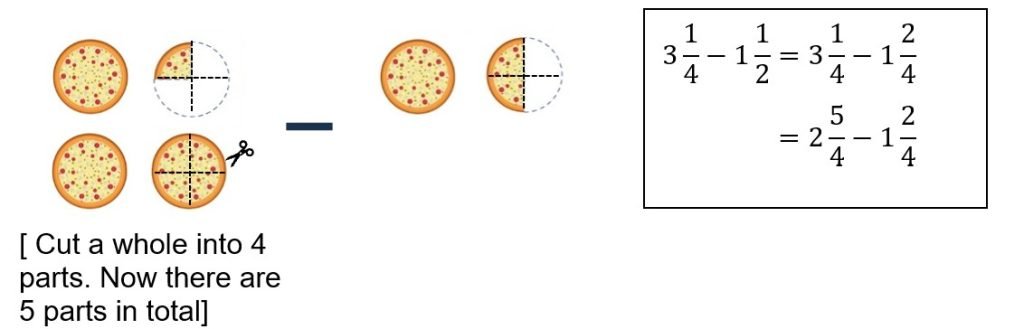
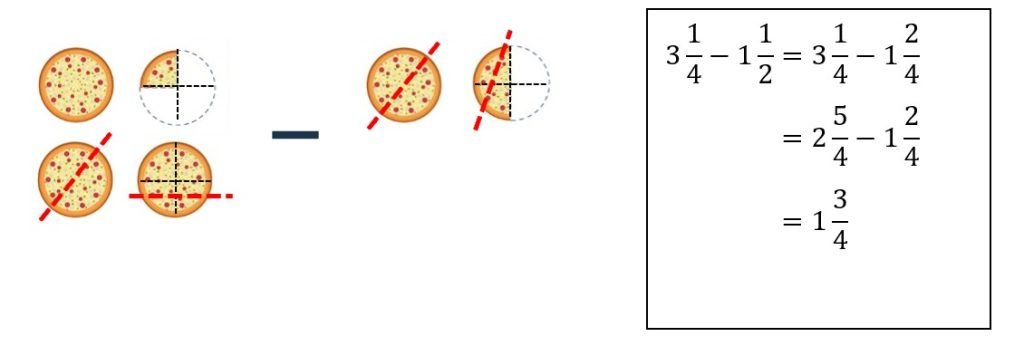
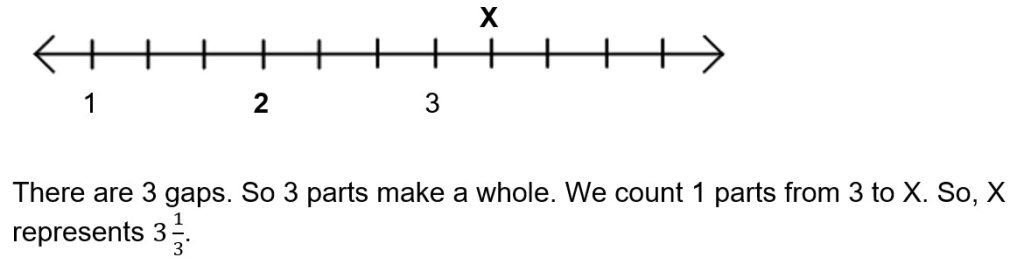
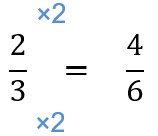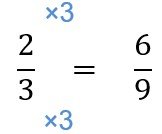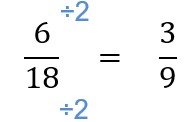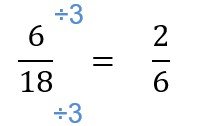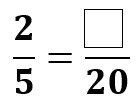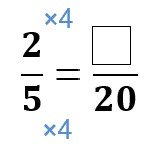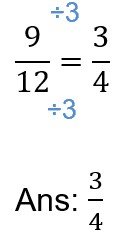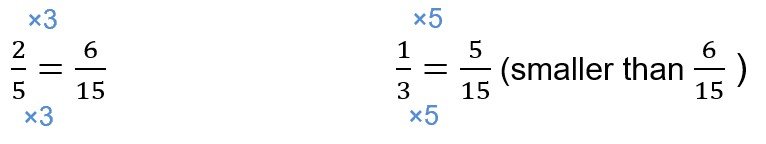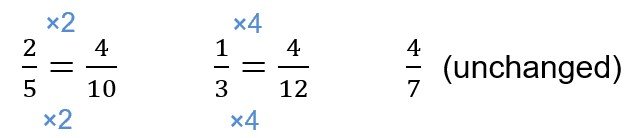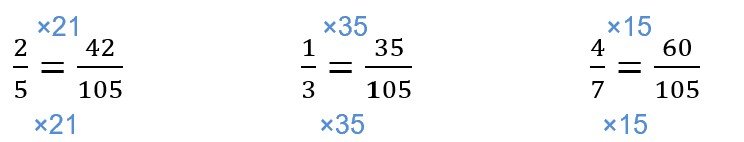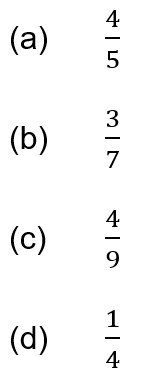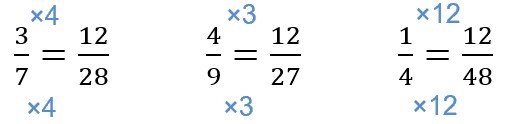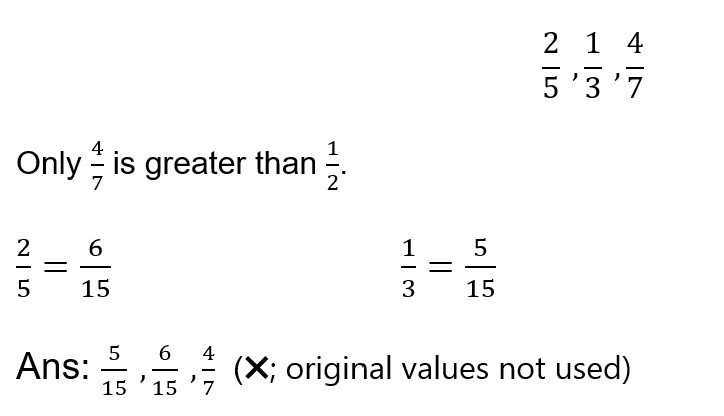Key Concept 5: Comparing and ordering of like and unlike fractions
When fractions are like, they have the same denominators. For example, 2/5 and 4/5 are like fractions. We can compare like fractions easily. Since 4/5 is made up of 4 parts while 2/5 is made up of 2 parts, we say 4/5 is greater than 2/5.
When fractions are unlike, they have different denominators. For example, 2/5 and 3/7 are unlike fractions. When fractions are in different denominators, it can be difficult to tell which is greater. This is because the parts in both fractions are expressed in different sizes.
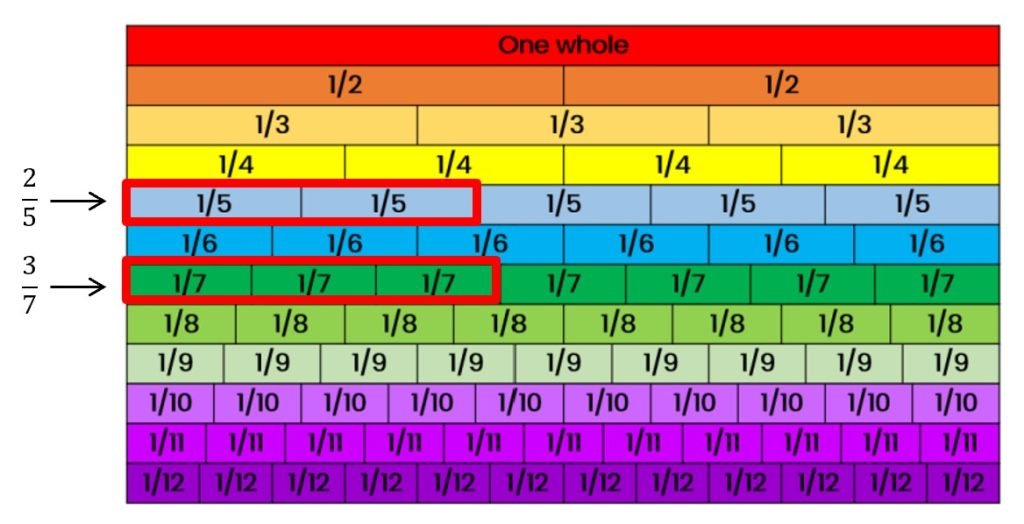
Using the fraction bars above, we can see that 3/7 is greater than 2/5. But we do not always have the diagram above to refer to. Furthermore, the diagram is limited to denominators up to 12. This means, the diagram will not be useful when we need to compare fractions with denominators larger than 12. For instance, 5/14 and 6/17.
To compare fractions expressed in different denominators, we can use one or a combination of the following methods:
(1) Comparing fractions with 1/2
(2) Expressing fractions in the same denominator
(3) Expressing fractions in the same numerator
Method 1: Comparing Fractions with 1/2
Fractions that are greater than 1/2 must be greater than fractions which are less than 1/2. We use 1/2 as a comparison point because it is convenient and easy to work with.
For example, when comparing 7/10 and 5/12:
See that the denominator of 7/10 is 10. So 1/2 = 5/10.
Comparing 7/10 and 5/10, we know 7/10 is greater than 1/2.
See that the denominator of 5/12 is 12. So 1/2 = 6/12.
Comparing 5/12 and 6/12, we know 5/12 is less than 1/2.
Ordering the fractions from smallest to greatest, we have:
5/12 , 1/2 , 7/10
So 7/10 is greater than 5/12.
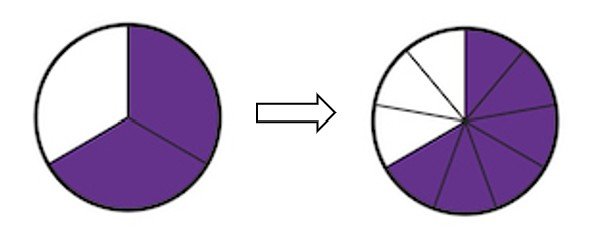
Method 2: Expressing fractions in the same denominator
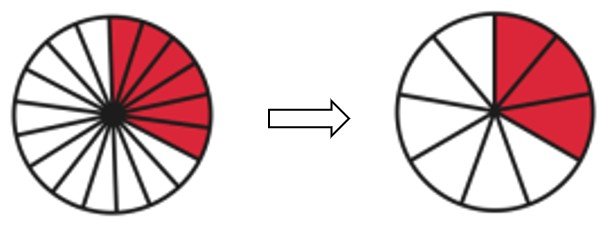
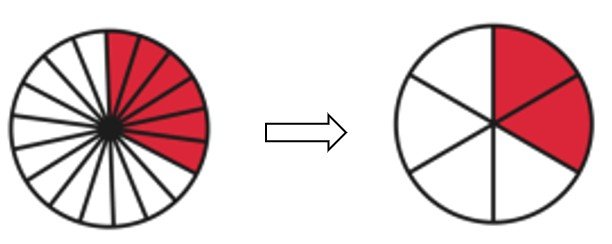
Recall that fractions with the same denominators are like fractions. When comparing fractions that are like, the greater the numerator, the greater the fraction. For instance, 4/5 is greater than 2/5 .
For example, when asked to compare 7/10 and 3/5, observe that the previous Method 1 of comparing to 1/2 would not be useful since both fractions are greater than 1/2 (half of 10 is 5; and half of 5 is 2.5).
However when we express 3/5 = 6/10, we see that 7/10 and 6/10 are like fractions, and 7 is greater than 6.
So we know 7/10 is greater than 3/5.
Further example:
Arrange the following fractions from the smallest to the largest.
2/5 , 1/3 , 4/7
Solution:
Apply Method 1 first and we can quickly see that 4/7 is greater than 1/2, while 2/5 and 1/3 are smaller than 1/2. This means we only need to compare 2/5 and 1/3 since 4/7 is the greatest fraction.
The lowest common multiple of 5 and 3 is 15. Changing the fractions into common denominators, we have:
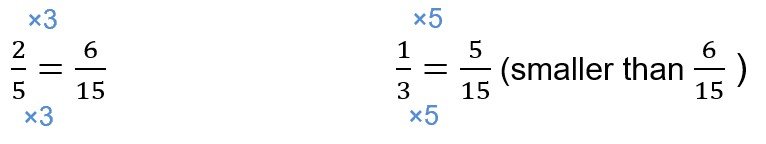
So our answer is 1/3 , 2/5 , 4/7 .
Method 3: Expressing fractions in the same numerator
Using the fraction bar diagram, we see that as the denominator of a fraction increases, its unit size becomes smaller.
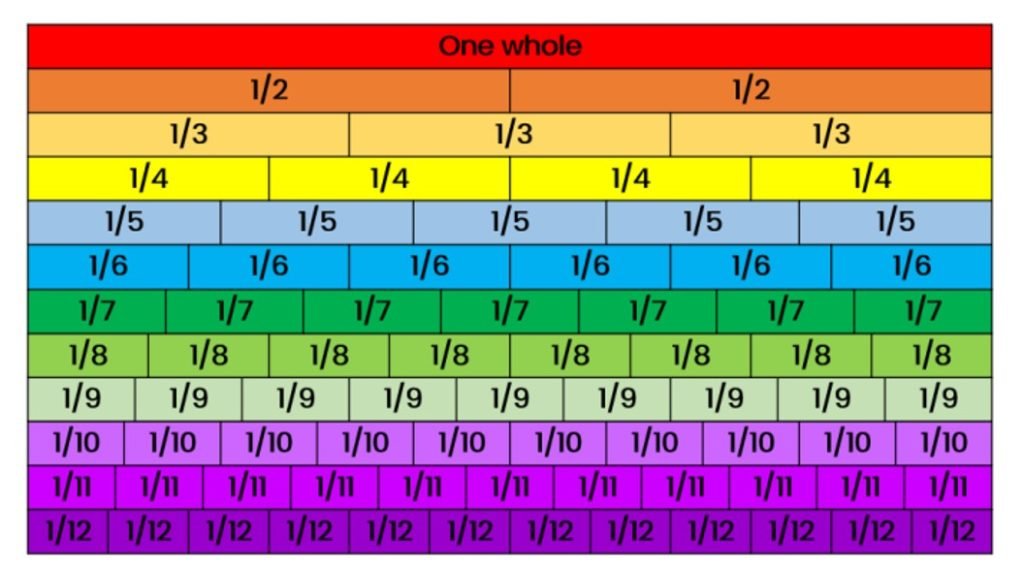
And so, when two fractions have the same numerator, the fraction with the smaller denominator is the fraction that is greater. For example, compare 2/5 , 2/4 and 2/5. See that all the fractions have the same numerator, but 2/3 is the greatest fraction since it has the largest unit size.
We use Method 3 when expressing the fractions into the same common denominator is difficult and tedious.
Let’s use the previous question as an example and apply Method 3.
Arrange the following fractions from the smallest to the largest.
2/5 , 1/3 , 4/7
Note that to express all the fractions into the same common denominator, we have to use 105 as the common denominator since the lowest common multiple of 3, 5 and 7 is 105. Three fractions must be changed.
However if we apply Method 3, then we have to only change 2/5 and 1/3 since the lowest common multiple of 1, 2 and 4 is 4, which is the numerator of 4/7.
Changing the fractions into common numerators, we have:
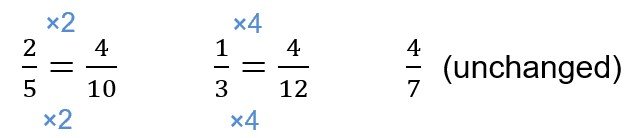
Arranging the fractions from the smallest to the greatest, we have: 1/3 ,2/5 , 4/7 .
*When we apply Method 3 in this case, numbers are easier to work with, as compared to applying Method 2 straight away on all the fractions:
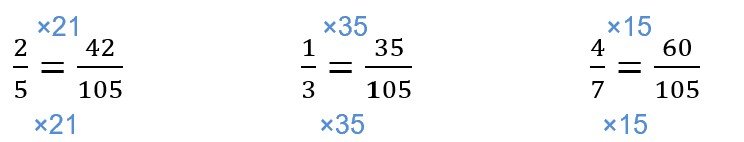
Examples of Comparing and Ordering Fractions
1. Arrange the following fractions from the smallest to the greatest.
3/5 , 7/10 , 2/4
Suggested Solution:
See that 2/4 = 1/2. Applying Method 1, both 3/5 and 7/10 are greater than 1/2. So 1/2 is the smallest fraction.
Comparing 3/5 and 7/10, the common denominator to use is 10.
3/5 = 6/10
Arranging from the smallest to the greatest, we have: 2/4 , 3/5 , 7/10. (ans)
2. Which of the following fractions is the smallest?
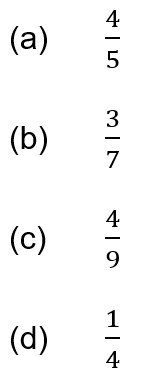
Suggested Solution:
Applying Method 1, only 4/5 is greater than 1/2. So we can eliminate option (a) since it cannot be the smallest fraction.
Comparing 3/7 , 4/9 and 1/4, the lowest common multiple for the denominators is 252. which is too big (but still possible to use). The lowest common multiple for the numerators is 12 (easier to use than 252).
Let’s use Method 3.
Changing the fractions into common numerators, we have:
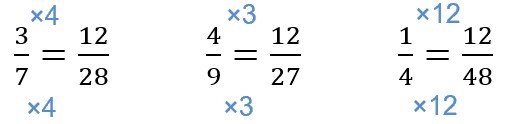
So, the smallest fraction is (d) 1/4. (ans)