Complete Vectors: O-Level Notes for Secondary Students (2025)

Introduction to Vectors

Vectors are essential tools in mathematics, representing quantities that have both direction and magnitude. Unlike a scalar quantity, which only has size (like temperature or mass), a vector combines both size and direction to give a fuller picture of physical quantities. For instance, if you’re calculating the distance and direction of a moving object, a vector can tell you both how far it travels (the magnitude of the vector) and where it’s headed (the direction of the vector).

Scalars and Vectors

A vector has both magnitude and direction but a scalar only has magnitude.

A unit vector is a vector with a magnitude of one, often used to indicate direction without affecting magnitude.

For example, a car has a speed of 90 km/h but a velocity of 90 km/h northwest.
(Speed is a scalar but velocity is a vector. Speed is the magnitude of the velocity.)

Other examples:

Representation of Vectors

• A vector is represented by a line segment.
  o The length of the line segment represents the magnitude of the vector.
  o The arrows on the line segment indicates the direction of the vector.
  
• The vector below is denoted by \(\overrightarrow{PQ}\) or a. The direction of the arrow represents the direction of the vector where P is the initial point and Q is the terminal point.
  (In your workings, your write instead of a.)

Magnitude of Vectors

Magnitude of  \(\overrightarrow{PQ}\) = length of \(\overrightarrow{PQ}\) = |\(\overrightarrow{PQ}\)| = |a| = .

For the vector \(\overrightarrow{PQ}\) on page 1, |\(\overrightarrow{PQ}\)| = 100.

The magnitude of a column vector \(\overrightarrow{AB}\) = b = \(\begin{pmatrix} x \\ y \end{pmatrix}\) is given by

                                                               |\(\overrightarrow{AB}\)| = |b| = √x² + y².

Equal Vectors

Two vectors are equal if they have the same magnitude and same direction.

i.e. \(\overrightarrow{AB}\) = \(\overrightarrow{CD}\) so AB is parallel to CD and |\(\overrightarrow{AB}\)| = |\(\overrightarrow{CD}\)|.

Negative Vectors

Two vectors are negative vectors of each other is they have the same magnitude but opposite direction. 

i.e. \(\overrightarrow{AB}\) = – \(\overrightarrow{BA}\) OR \(\overrightarrow{BA}\) = – \(\overrightarrow{AB}\)

a = – (– a)               – a = – ( a)

Regardless,  |\(\overrightarrow{AB}\)| = |\(\overrightarrow{BA}\)|.

Addition and Subtraction of Vectors

The addition/subtraction of two vector quantities results in a new vector quantity, combining both magnitude and direction.

Vector Addition

The principle of adding two vectors can be extended to more than two vectors.

Vector Subtraction

The principle of subtracting two vectors can be extended to more than two vectors.

Zero Vector

Given any vector p, there exists a negative vector ‒p such that

p + (– p) = (– p) + p = 0

0 is a zero vector that can also be written as .

• It is not a scalar (different from scalar zero, 0) because the resultant addition/subtraction of two or more vectors must be a vector.
• It has zero magnitude and no specific direction – it is represented by a point.
• When a zero vector is added or subtracted from any vector, the latter remains unchanged.

Scalar Multiplication

When vector a is multiplied by scalar k, the resulting vector has magnitude k times of a,

|ka| = k |a|.

• When , k>0, ka is a vector with the same direction as a and a magnitude that is k times of a.

• When, k<0, ka is a vector with the opposite direction as a and a magnitude that is k times of a.

• When, k = 0, ka is a zero vector.

In general, for any vector a and b, and real numbers m and n, then

• m (na) = n (ma) = (mn) a
• ma + na = a (m + n)
• ma + mb = m (a + b)

Parallel Vectors

• If a = kb , where k is a scalar and k≠0, then a is parallel to b and |a| = k |b|.
• If a is parallel to b, then a = kb where k is a scalar and k ≠ 0.

Collinear Points

If points A, B and C lie in a straight line (i.e. they are collinear), then \(\overrightarrow{AB}\) = k\(\overrightarrow{BC}\).

Position Vectors

The position vector of any point is the vector from the origin to that point. Position vectors can be expressed in terms of their horizontal direction (x-axis) and vertical direction (y-axis) components.

For example, \(\overrightarrow{OP}\)  is the position vector of P relative to O.

If point P has coordinates (a, b) , then the position vector of P, \(\overrightarrow{OP}\) is written as \(\begin{pmatrix} a \\ b \end{pmatrix}\).

For any two points P and Q, \(\overrightarrow{PQ}\)  is the position vector of Q relative to P.

\(\overrightarrow{PQ}\) = \(\overrightarrow{PO}\) + \(\overrightarrow{OQ}\) = \(\overrightarrow{OQ}\) – \(\overrightarrow{OP}\)

\(\overrightarrow{PQ}\) is also known as a translation vector because the vector can be regarded as a movement from P to Q.

Addition

For column vectors,

\(\begin{pmatrix} p \\ q \end{pmatrix} + \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} p+r \\ q+s \end{pmatrix}\)

Notice that

• A\((p,q)\), B\((r,s)\) and C\((p+r,q+s)\),
• \(\overrightarrow{OA} =\begin{pmatrix} p \\ q \end{pmatrix}, \overrightarrow{OB} = \begin{pmatrix} r \\ s \end{pmatrix} and \overrightarrow{OC} = \begin{pmatrix} p+r \\ q+s \end{pmatrix}\),
• OACB is a parallelogram.

Subtraction

For column vectors,

\(\begin{pmatrix} p \\ q \end{pmatrix} – \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} p-r \\ q-s \end{pmatrix}\)

Notice that

• A\((p,q)\), B\((r,s)\) and C\((p-r,q-s)\),
• \(\overrightarrow{OA} =\begin{pmatrix} p \\ q \end{pmatrix}, \overrightarrow{OB} = \begin{pmatrix} r \\ s \end{pmatrix} and \overrightarrow{OC} = \begin{pmatrix} p-r \\ q-s \end{pmatrix}\),
• \(\overrightarrow{OA} = \mathbf{0}\), \(\overrightarrow{OB} = \mathbf{a}\) and \(\overrightarrow{OC} = \mathbf{b}\).

Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later. 

This will be delivered to your email inbox.

Click here to download

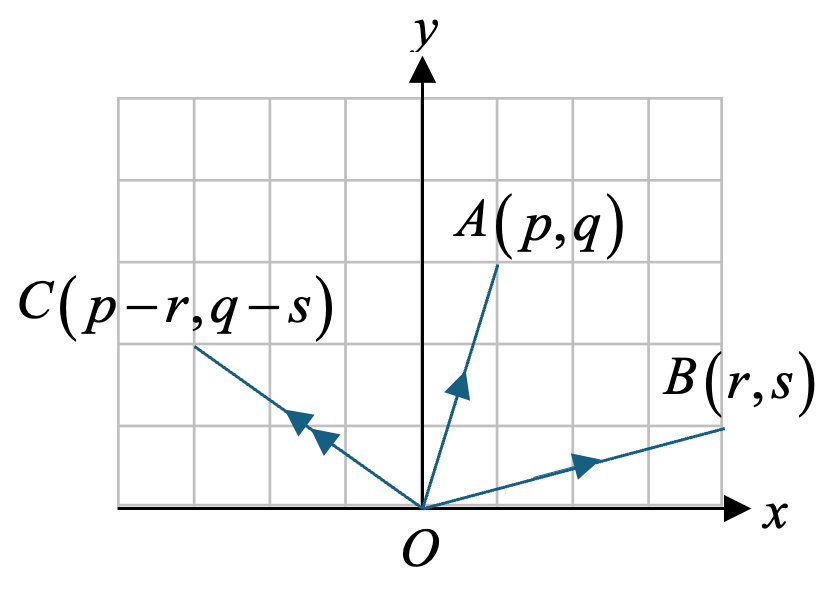
Does your child need help with Vectors in Math?

Find out more about our Math Tuition Class Free Trial.

To learn more about the various subjects we cover, click here to find out more about our A-Maths tuition options, or check out our A-Maths revision notes.

1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:

– Live Zoom lessons
– Adaptably, a smart learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital questions.
– 24/7 Homework Helper Service

We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities. We also offer a free trial class and consultation with our tutors, to help make sure we are the best fit for your child.

We specialise in English, Math, Science, and Chinese subjects.

You can see our fees and schedules here >>

Primary Math Tuition

Secondary Math Tuition

2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.

Your child can:

– Learn from recorded videos

– Get access to lots of common exam questions to ensure sufficient practice

– Get unlimited support and homework help

You can see the available courses here >>

Math Online Courses