In these revision notes, you will learn the following:
- Basics of Trigonometric Ratios
- Finding ratios for Special Angles
- Applications
Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.

Basics of Trigonometric Ratios
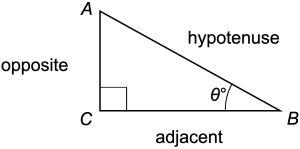
At the heart of trigonometry are the three primary trigonometric ratios: sine, cosine, and tangent. These ratios are defined for acute angles in a right triangle but can be extended to larger angles. Here is a quick recap of their definitions:
Sine (sin θ): The ratio of the length of the opposite side to the hypotenuse.
Cosine (cos θ): The ratio of the length of the adjacent side to the hypotenuse.
Tangent (tan θ): The ratio of the length of the opposite side to the adjacent side.
Note:
By taking the reciprocals of sin θ, cos θ and tan θ, we obtain the cosecant (cosec), secant (sec) and cotangent (cot) functions.
\[{\frac{1}{\text{sin}\theta} = \text{cosec}\theta,\ \text{sin}{\theta \neq 0}}\]
\[{\frac{1}{\text{cos}\theta} = \text{sec}{\theta,\ \ }\ \text{cos}{\theta \neq 0}}\]
\[{\frac{1}{\text{tan}\theta} = \text{cot}{\theta,\ }\ \text{tan}{\theta \neq}0}\]
The ratios work for any right−angle triangle. For example, in any right triangle, given one of the angles is 30° and \(\text{sin}{\text{30°}\text{ }\text{=}}\ \frac{\text{1}}{\text{2}}\), then the ratio of the length of the opposite side to the length of the hypotenuse must be \(\frac{\text{1}}{\text{2}}\) .
And so, we can use Pythagoras’ Theorem to obtain the length of the adjacent side:
\[\sqrt{\text{2}^{\text{2}}\ – \text{ }\text{1}^{\text{2}}}\text{ }\text{=}\text{ }\sqrt{\text{3}}\text{ units}\]
Hence, we will be able to obtain the ratios and \({\text{cos}\text{30°}}\text{ =}\text{ }\frac{\sqrt{\text{3}}}{\text{2}}\) and \(\text{tan}{\text{30°}\text{ }\text{=}}\ \frac{\text{1}}{\sqrt{3}}\) .
Introduction to Special Trigonometric Angles
Consider the equation:
\[\text{sin}{\text{30°}\text{ }\text{=}}\ \frac{\text{1}}{\text{2}}\]
Note that the slightest change in the magnitude of the angle will no longer give an exact sine value. For example, sin 30.0001º = 0.5000015…, and sin 29.9999º = 0.4999984…
Most of the angles in trigonometric functions give us irrational numbers because of the square root mechanic from Pythagoras Theorem in the calculations of the sides of the triangle. Since the value of \(\text{sin}{\text{30°}\text{ (}\text{=}}\ \frac{\text{1}}{\text{2}})\), is an exact value that can also be easily remembered, we say that 30º is a special trigonometric angle.
Other special trigonometric angles where the trigonometric ratios give simple, exact values include 0° (or 360º), 45°, 60°, 90°, 180º and 270º
What makes these angles special? The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots (surds) of simple numbers. These angles arise naturally in geometric constructions and have straightforward trigonometric values due to symmetry.
Deriving Values for Special Trigonometric Angles : 30º and 60º

Consider the equilateral triangle ABC above. AM ⊥ BC, and M is the midpoint of BC, such that BM : MC = 1 : 1.
For ease of calculation of BM, let each side of the equilateral triangle be 2 units, then BM = 1 unit. Since AM is the angle bisector of ∠BAC, then ∠BAM = 60º ÷ 2 = 30º.
Observe that in right−angled triangle BAM,
| \[\text{sin}{\text{30°}\text{ }\text{=}}\ \frac{\text{1}}{\text{2}}\] | \[\text{sin}\text{60° =}\text{ }\frac{\sqrt{\text{3}}}{\text{2}}\] |
| \[\text{cos}\text{30° =}\ \frac{\sqrt{\text{3}}}{\text{2}}\] | \[\text{cos}\text{60° =}\text{ }\frac{\text{1}}{\text{2}}\] |
| \[\text{tan}\text{30° =}\ \frac{1}{\sqrt{\text{3}}}\] | \[\text{tan}\text{60° =}\text{ }\sqrt{\text{3}}\] |
Deriving Values for Special Trigonometric Angle: 45º

Consider the right−angled isosceles triangle ABC above where AM : BC = 1 : 1.
Observe that in right−angled isosceles triangle ABC,
\[\text{sin}\text{45° =}\text{ }\frac{\text{1}}{\sqrt{\text{2}}}\]
\[\text{cos}\text{45° =}\text{ }\frac{\text{1}}{\sqrt{\text{2}}}\]
\[\text{tan}\text{45° =}\text{ }\text{1}\]
Tips to Recall Special Trigonometric Angles: 30º, 45º and 60º
| 30° (or \(\frac{\mathbf{\pi}}{\mathbf{6}}\) rad) | 45° (or \(\frac{\mathbf{\pi}}{\mathbf{4}}\) rad) | 60° (or \(\frac{\mathbf{\pi}}{\mathbf{3}}\) rad) | |
|---|---|---|---|
| sin | |||
| cos | |||
| tan |
Construct a table as shown above. Write out sine, cosine and tangent on the first vertical column, and fill in 30º, 45º and 60º on the first horizontal as shown above.
For the second row (sine), write ‘1’ , ‘2’ and ‘3’, in each of the respective cells and write ‘3’, ‘2’, ‘1’, in the row below for cosine.
Add a square root for each number in the cells and then add a denominator of 2 for each cell.
You have now obtained all the special values for the trigonometric ratios of sine and cosine. What about tangent? Recall that \(\tan{\theta =}\frac{\sin\theta}{\cos\theta}\). To obtain the values for tangent, simply divide the numerator for sine by the numerator for cosine. You should get the following:
| 30° (or \(\frac{\mathbf{\pi}}{\mathbf{6}}\) rad) | 45° (or \(\frac{\mathbf{\pi}}{\mathbf{4}}\) rad) | 60° (or \(\frac{\mathbf{\pi}}{\mathbf{3}}\) rad) | |
|---|---|---|---|
| sin | \[\frac{1}{2}\] | \[\frac{\sqrt{2}}{2}\] | \[\frac{\sqrt{3}}{2}\] |
| cos | \[\frac{\sqrt{3}}{2}\] | \[\frac{\sqrt{2}}{2}\] | \[\frac{1}{2}\] |
| tan | \[\frac{1}{\sqrt{3}}\] | 1 | \[\sqrt{3}\] |
*For other trigonometric ratios such as secant, cosecant and cotangent, simply take the reciprocal. For example, secant is the reciprocal of cosine.
So sec 30° = 1 ÷ co 30° = 1 ÷ \(\frac{\sqrt{3}}{2}\) = \(\frac{2}{\sqrt{3}}\)
Deriving Values for Special Trigonometric Angles: 0º (360º), 90º, 180º and 270º
Values for special trigonometric angles that are acute can be easily obtained when the angles can be designated in a right−angled triangle. However, it may be difficult to visualise the sine of 0º and º90 since the two smaller angles in a right−angled triangle cannot be 0º or 90º. It is also not possible contain 180º and 270º in a right−angled triangle. As such, a more direct way to obtain the values for special trigonometric angles of 0º (360º), 90º, 180º and 270º would be to recall the respective basic trigonometric graphs. We only need to sketch the graph for 0º to 360º.
The Sine Graph
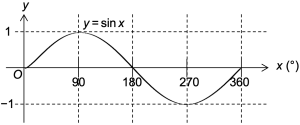
From the sine graph above, we can easily see that
| sin 0º = 0 | sin 90º = 1 | sin 180º = 0 | sin 270º = -1 |
| sin 360º = 0 |
The Cosine Graph

From the cosine graph above, we can easily see that
| cos 0º = 1 | cos 90º = 0 | cos 180º = -1 | cos 270º = 0 |
| cos 360º = 1 |
The Tangent Graph

From the tangent graph above, we can easily see that
| tan 0º = 0 | tan 90º = undefined | tan 180º = 0 | tan 270º = undefined |
| tan 360º = 0 |
*For other trigonometric ratios such as secant, cosecant and cotangent, simply take the reciprocal. For example, cosec is the reciprocal of sine.
So cosec 90° = 1 ÷ sin 90° = 1 ÷ 1 = 1
Simplification of Calculations
Knowing the values of special trigonometric angles simplify calculations, making them particularly useful for both theoretical work and practical applications.
When solving trigonometric equations or proving identities, knowing the exact values removes the need for approximation of irrational numbers.
Example 1
Using addition formula, find the exact value of sin 105.
Solution:
\[\text{sin}{105{^\circ} = \sin(60{^\circ} + 45{^\circ})}\]
\[= \sin{60{^\circ}}\cos{45{^\circ}} + \cos{60{^\circ}}\sin{45{^\circ}}\]
\[= \frac{\sqrt{3}}{2} \times \frac{\sqrt{2}}{2} + \frac{1}{2} \times \frac{\sqrt{2}}{2}\]
\[= \frac{\sqrt{6} + \sqrt{2}}{4}\ \ \text{(}\text{ans}\text{)}\]
Example 2
Show that tan 45º × sec 60º = 2.
Solution:
\[\tan{45{^\circ}} \times \sec{60{^\circ}} = \tan{45{^\circ}} \times \frac{1}{\cos{60{^\circ}}}\]
\[= 1 \times \frac{1}{0.5}\]
\[= 2\ \ \text{(}\text{ans}\text{)}\]
Example 3
Solve \((2\text{sin}^{2\ }x\ + \ \sin x – 1) = 0\), for \(0{^\circ} \leq x \leq 360{^\circ}\).
Solution:
\[\left( 2\text{sin}^{2\ }x + \ \sin x – 1 \right) = 0\]
\[\left( 2\sin x – 1 \right)\left( \sin x + 1 \right) = 0\]
\[\sin x = \frac{1}{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{Or }\sin x\text{=}\ – 1\ \text{(no basic angle)}\]
\[\text{Basic}\ \measuredangle = 30{^\circ}\ (x\text{ is in 1st or 2nd quadrant Or }\text{ }x\text{ = 270°}\ (\text{from graph)}\text{}\]
\[x = 30{^\circ}\ ,\ 150{^\circ}\]
Ans: 30°, 150° or 270°
Applications of Special Trigonometric Angles
Special trigonometric angles, such as 30°, 45° and 60°, have specific trigonometric values that are widely used in various fields due to their simplicity and ease of calculation. These angles find application in numerous disciplines, from mathematics and physics to engineering and architecture. Below are some key applications of special trigonometric angles in different fields:
1. Engineering
Structural Design: Engineers often use special trigonometric angles to determine forces in structural components, such as beams, trusses, and cables. For example, in bridge design, these angles help calculate load distributions and stress on different parts of the structure.
Electrical Engineering: Special angles are essential in analysing alternating current (AC) circuits, where sinusoidal functions model the behaviour of currents and voltages. Phasor diagrams, which represent the magnitude and phase of these functions, commonly use 30°, 45° and 60° to simplify circuit analysis.
Mechanical Engineering: In kinematics and dynamics, these angles are used to calculate trajectories, forces, and torques in mechanical systems, especially when dealing with inclined planes, gears, and linkages.
2. Physics
Projectile Motion: Special angles play a significant role in solving problems related to projectile motion, where the angle of launch is a crucial factor in determining the range, height, and time of flight of a projectile.
Optics: In the study of light and lenses, special trigonometric angles are used in calculating the angle of incidence, reflection, and refraction. The use of these angles simplifies the derivation of the laws of reflection and refraction.
Wave Mechanics: Special angles are used in the study of wave interference, diffraction, and standing waves. These angles often simplify the calculation of phase differences, wave intensities, and resonance conditions.
3. Architecture
Roof Design: Architects use special angles in the design of roof trusses and inclined structures. For example, the common roof pitch often involves angles such as 30° and 45°, which help in determining the optimal slope for drainage and aesthetics.
Geometric Proportions: Special trigonometric angles help architects create precise geometric proportions in buildings. For example, angles like 45° are frequently used in the design of facades, staircases, and windows to maintain symmetry and balance in architectural designs.
4. Computer Graphics
3D Modelling and Animation: In computer graphics, special angles are often used in transformations such as rotations, scaling, and perspective projections. For example, rotations by 45° or 60° are common in 3D rendering, where trigonometric functions are used to rotate objects and calculate viewing angles.
Game Development: Special angles help in collision detection, movement algorithms, and physics simulations in game development. Trigonometric calculations based on these angles simplify the modelling of character movement, camera angles, and environmental interactions.
5. Robotics
Kinematics: In robotics, special trigonometric angles are crucial for calculating joint angles and positions of robotic arms and manipulators. For example, inverse kinematics, which determines the necessary joint angles for a robot to reach a specific position, often utilises angles like 30° and 45° to simplify the computation.
Path Planning: Robots use special angles to navigate their environment, avoid obstacles, and determine optimal paths. These angles are used to calculate turning angles and sensor positions to ensure accurate movement and detection.
Conclusion
From engineering to architecture, physics to computer graphics, these angles facilitate everything from structural analysis to the rendering of 3D models. Moreover, their use in robotics and wave mechanics underscores their importance in cutting-edge technology and innovation. By understanding these special angles and their properties, one gains not only a deeper appreciation of trigonometry but also a powerful set of tools to apply in practical and theoretical contexts.
Further Practice
Here are some practice questions for you to try.
Here are some practice questions for you to try.
Q1. Find the exact value of \(\frac{\tan{225{^\circ}}}{\sin{300{^\circ}} + \cos{120{^\circ}}}\) .
Q2. Solve sin2 θ cos θ = 2 sin θ cos θ, for 0 ≤ θ ≤ π.
Q3. Solve sin2 2x = − sin x cos x, for −π ≤ x ≤ π
Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.

Does your child need help in his or her studies?
Find out more about our Math Tuition Class Free Trial.
1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:
– Live Zoom lessons
– Adaptably, a smart learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital questions.
– 24/7 Homework Helper Service
We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities. We also offer a free trial class and consultation with our tutors, to help make sure we are the best fit for your child.
We specialise in English, Math, Science, and Chinese subjects.
You can see our fees and schedules here >>
2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.
Your child can:
– Learn from recorded videos
– Get access to lots of common exam questions to ensure sufficient practice
– Get unlimited support and homework help
You can see the available courses here >>
