Rate of Water Flow Question (Involving Volume Dimensions)
The primary goal of this math revision note is to enhance your child’s proficiency in solving rate of water flow questions involving volume dimensions and proportionate heights.
These questions assess your child’s understanding of rate and volume.
Before you read on, you might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.
This will be delivered to your email inbox.
Rate of Water Flow (Volume Dimension) Question 1
The figure shows taps A and B with two empty tanks A and B.
Both taps are turned on at the same time.
Water flowed from tap A into tank A at a rate of 5 litres per minute.
(a) What should the rate of flow of water be from tap B such that the height of water is the same for both tanks after some time?
(b) What should the rate of flow of water be from tap B such that the height of water in tank A is twice that of tank B after some time?
Solutions for (a)
Base area of Tank A = 70 cm × 50 cm = 3500 cm2
Base area of Tank B = 84 cm × 50 cm = 4200 cm2
Since the question requires the height of water to be the same, we can set this height as 1u.
For every 5 units of water in Tank A, there must be 6 units of water in Tank B in order for the height of water in both tanks to be the same.
The rate of water flow of Tap A is 5 litres per minute.
This means that in the 1-minute time frame, 5 litres of water have entered Tank A. For the water in Tank B to have the same height, there should be 6 litres of water that have entered Tank B in this 1-minute time frame.
5 u = 5 litres per minute
1 u = 1 litres per minute
6 u = 6 litres per minute (Ans)
Solutions for (b)
Since the question requires the height of water in tank A to be twice of that in tank B, we can set the height of water in Tank A to be 2u while the height of water in tank B to be 1u.
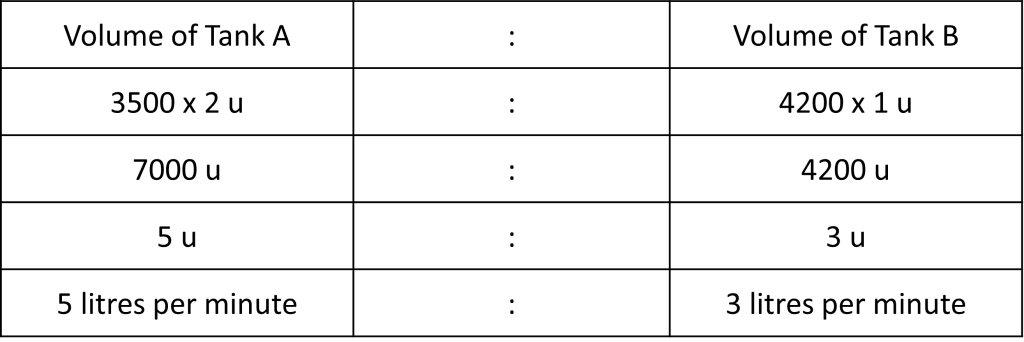
5 u = 5 litres per minute
3 u = 3 litres per minute (Ans)
Alternative solutions for (b)
From (a), we know that for the water in both tanks to have the same height, Tap B’s rate has to be 6 litres per minute while Tap A’s rate is 5 litres per minute.
So, for the water in Tank A to have double the height of the water in Tank B, Tap B just need to produce half as fast as before or half as productive as before.
Hence the rate of Tap B = 6 ÷ 2
= 3 litres per minute (Ans)
Test your child’s understanding by taking this short quiz!
Click the button below.
Before you go, you might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.
This will be delivered to your email inbox.
Does your child need help in his or her studies?
1) Live Zoom Lessons at Grade Solution Learning Centre
At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:
– Live Zoom lessons
– Adaptably™, an innovative smart learning platform featuring thousands of PSLE and exam-based questions tailored for your child’s practice. Adaptably not only tracks your child’s progress but also identifies their strengths and areas for improvement, providing valuable insights to enhance their learning journey.
– 24/7 Homework Helper Service
We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.
We specialise in English, Math, Science and Chinese subjects.
You can see our fees and schedules here >>
2) Pre-recorded Online courses on Jimmymaths.com
If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.
Your child can:
– Learn from recorded videos
– Get access to lots of common exam questions to ensure sufficient practice
– Get unlimited support and homework help
You can see the available courses here >>