In this Parallelogram Formula Guide, we go over the key principles of this vital shape in Mathematics, as well as its properties and applications.
Before you read on, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.

Definition of a Parallelogram
A parallelogram is a quadrilateral (a closed, four−sided shape), such that
(i) both pairs of opposite sides are parallel, AND
(ii) opposite sides of a parallelogram are of equal length.
The following are some examples of parallelograms.

Note that Figure 1 is the most common representation of parallelograms. We can think of parallelograms as slanted rectangles. Additionally, squares (Figure 2), rhombuses (Figure 3) and rectangles (Figure 4) are also considered to be parallelograms based on the definition of a parallelogram above.
The following are non−examples of parallelograms.
Calculating the Area of a Parallelogram
Consider the parallelogram below, with base, b, and vertical height, h. Note that the vertical height, h, is also known as the shortest distance between the parallel sides.
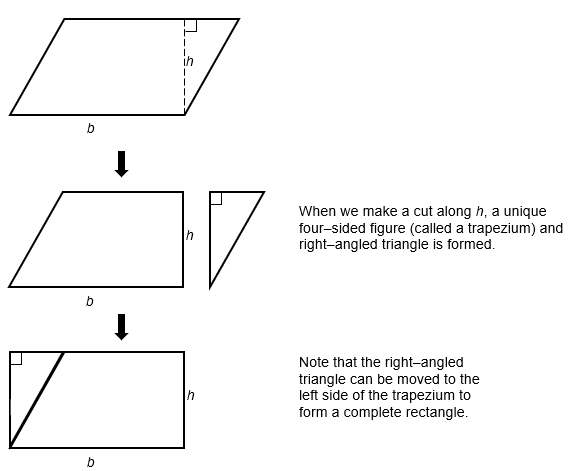
Since the area of the original parallelogram and the area of the newly formed rectangle are the same, we can infer that the formula to calculate the area of the parallelogram and the formula to calculate the area of the rectangle is also the same.
Parallelogram Formula
Hence area of a parallelogram = base (b) × height (h)
Example 1
The diagram below shows a parallelogram, ABCD. AB = 12 cm and vertical height of the parallelogram is 8 cm. What is the area of ABCD?
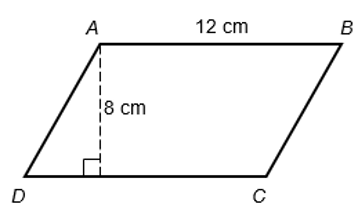
Solution:
Area of ABCD = 12 cm × 8 cm = 96 cm2 (Ans)
Example 2
The diagram below shows a parallelogram, PQRS. PQ = 20 cm and the shortest distance between PS and QR is 16 cm. What is the area of PQRS?
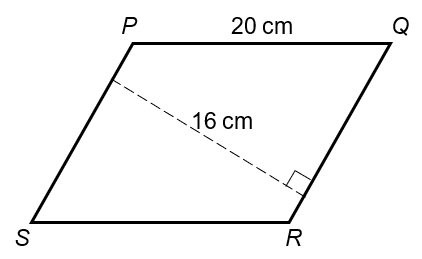
Solution:
Area of PQRS = 20 cm × 16 cm = 320 cm2 (Ans)
Example 3
The diagram below shows a parallelogram, ABCD. Given that AB = 15 cm and the area of ABCD is 135 cm2 . What is the length of h?
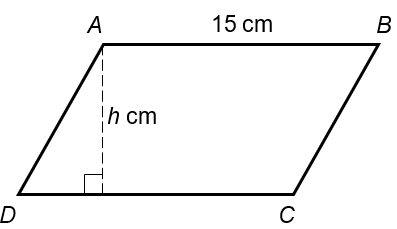
Solution:
Area of ABCD = 15 cm × h cm = 135 cm2
h = 135 ÷ 15 = 9 cm (Ans)
Key Properties of Parallelograms
Parallelograms possess several geometric and angle properties that distinguish them from other shapes.
Geometric Properties:
Consider the parallelogram, ABCD, below.
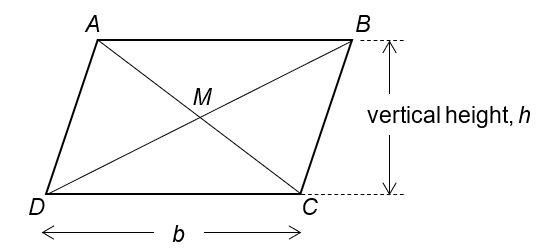
1. Opposite sides are parallel and congruent (identical):
This is the defining feature of a parallelogram. Opposite sides are parallel and have the same length. Hence AB // CD, AD // BC, AB = CD, and AD = BC.
2. Diagonals bisect each other:
The diagonals (AC and BD) of a parallelogram cross each other at their midpoints. This means the two diagonals divide each other into two equal parts at M. Hence AM = CM and BM = DM.
3. Area is determined by the base and height:
The area is given by the formula, Area = base (b) × height (h)
4. Its diagonals bisect the parallelogram into two identical triangles:
Because opposite sides of a parallelogram are equal, each diagonal will bisect the parallelogram into two triangles that are identical.
Hence, ∆ACD is identical to ∆ACB, and ∆BDA is identical to ∆BDC.
Furthermore, ∆AMB is identical to ∆CMD, and ∆AMD is identical to ∆CMB.
5. Deriving coordinates of the vertex of a parallelogram:
Opposite sides of a parallelogram are equal and the distance between each pair of parallel lines is constant. Therefore in the context of coordinate geometry, we can always derive the last pair of coordinates of a parallelogram when the coordinates of all other three points are known.
Example
ABCD are points on the cartesian plane such that ABCD form a parallelogram. State the coordinates of point B.
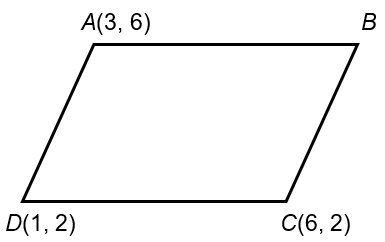
Solution:
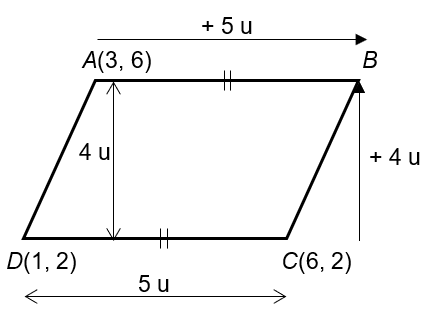
The horizonal gap between D and C is the same as the horizontal gap between A and B. The horizontal gap is 6 – 2 = 4 units. So the x−coordinate for B is 3 + 5 = 8,
The vertical gap between A and D is the same as the horizontal gap between B and C. The horizontal gap is 6 – 2 = 4 units. So the y−coordinate for B is 2 + 4 = 6.
So the coordinates for B are (8, 6). (Ans)
Angle Properties:
Consider the parallelogram, ABCD, below
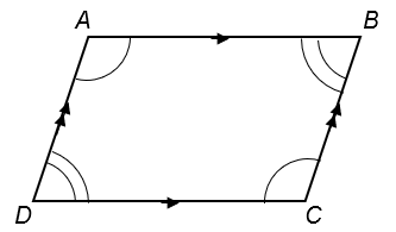
1. Opposite angles are equal:
Angles facing each other across the shape are equal. This property is covered at the primary level. See that:
∠BAD = ∠BCD
∠ADC = ∠ABC.
2. Consecutive angles are supplementary:
Any two angles adjacent to each other add up to 180°. This property is covered at the primary level. See that:
∠BAD + ∠ADC = 180°
∠ADC + ∠BCD = 180°
∠BCD + ∠ABC = 180°
∠DAB + ∠ABC = 180°
3. Sum of all interior angles is 360°:
As with all quadrilaterals, the sum of the interior angles of a parallelogram is always 360°.
4. Diagonals in the parallelogram form alternate angles:
Because opposite sides of a parallelogram are parallel, diagonals in the parallelogram form alternate angles. Consider diagonal AC as shown below.
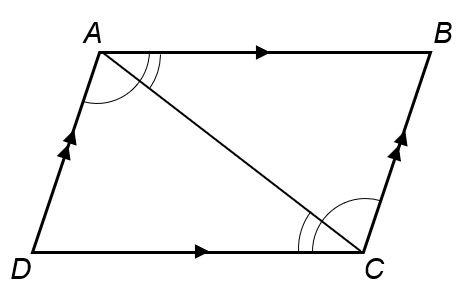
The alternate angles are:
∠BAC = ∠ACD (as a result of BA // CD)
∠DAC = ∠BCA (as a result of AD // BC)
Applications of Parallelograms
Parallelograms are used in various fields and everyday scenarios:
1. Architecture:
Parallelograms are used in the design of buildings, bridges, and tiles for symmetry and balance.

Name and location of building: Atelier for Calligrapher, Japan
2. Engineering:
They appear in mechanisms such as linkages, crane arms, and trusses for distributing forces evenly.
3. Art and Design:
Artists and designers use parallelograms to create visual effects, patterns, and perspectives.

Tessellation with the use of parallelograms
4. Sports:
In sports such as football, badminton and tennis, play areas are rectangular parallelograms to make the playing area even on both sides.
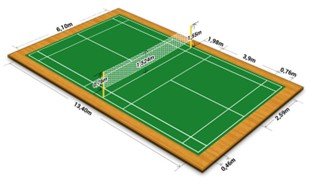
The official measurements of a professional badminton court
Frequently Asked Questions (FAQs)
1. What is the relationship between parallelograms and triangles?
Parallelograms and triangles share a close relationship because the diagonals of a parallelogram divide it into two congruent (identical) triangles. This property is used to solve problems related to symmetry, area, and geometric proofs.
2. Can a parallelogram have all unequal sides?
No, in a parallelogram, opposite sides must be equal in length. However, adjacent sides can have different lengths, as seen in a generic parallelogram (Figure 1 above).
3. How do the diagonals of a parallelogram behave?
The diagonals of a parallelogram bisect each other at their midpoints. This means that the point where they intersect divides each diagonal into two equal segments. Note that the diagonals do not intersect each other at right angles. This only applies to squares, rhombuses and kites.
4. Is a rhombus always a parallelogram?
Yes. A rhombus has equal sides, and both pairs of opposite sides are parallel. This matches the definition of a parallelogram.
5. Is a parallelogram always a rhombus?
No. A rhombus requires all four sides to be equal. This is not always the case in parallelograms.
6. Can a parallelogram contain right angles?
Yes. Note that if an angle in a parallelogram is a right angle, then all other angles in a parallelogram would also be right angles (by Angle Properties #2 above). This parallelogram would then be a rectangle or a square (if all four sides are equal).
Parallelogram Shape Rules and Formulas
Parallelograms are an essential part of geometry that you can find in both everyday life and advanced Maths problems.
They have unique properties that make them fun to study and practical to use. By learning about their shapes, properties, and calculations, you will build a strong foundation in geometry.
Keep practising, and look for parallelograms around you – they are everywhere!
To find out more about different subjects, check out our PSLE revision notes here, or find out more about our PSLE Math Tuition, where our experienced teachers help your child work through the Primary School Maths syllabus.
Need More Revision Notes for Primary School Math?
Check out our exam guide on other topics here!
Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.

Does your child need help with Mathematics?
1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:
– Live Zoom lessons
– Adaptably, an AI-Powered learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital questions.
– 24/7 Homework Helper Service
We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.
We specialise in English, Math, Science, and Chinese subjects.
You can see our fees and schedules here >>
2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.
Your child can:
– Learn from recorded videos
– Get access to lots of common exam questions to ensure sufficient practice
– Get unlimited support and homework help
You can see the available courses here >>
