Math Heuristics in Problem-Solving: A Parent’s Guide to Primary 4 Math

Why Are P4 Math Heuristics So Important?

Primary 4 marks a turning point where students transition from simple arithmetic to complex problem-solving. Here’s why heuristics matter for your P4 child:

Building Real-World Thinking Skills

P4 students learn to solve problems just like in real life – whether it’s sharing pocket money fairly, planning time for activities, or figuring out how many stickers to trade. These thinking skills transfer beyond mathematics.

Developing Mathematical Confidence

When P4 students master heuristics, they stop feeling stuck when facing unfamiliar problems. They gain multiple strategies to approach challenges, building the confidence essential for PSLE preparation.

Preparing for P5 and P6 Complexity

The heuristics learned in P4 become the foundation for more advanced problem-solving in upper primary. Students who master these strategies find P5 and P6 mathematics much more manageable.

Aligning with Singapore’s World-Class Curriculum

Singapore’s mathematics program emphasizes deep understanding over memorization. P4 heuristics teach students to think systematically and reason logically – skills that make Singapore students excel globally.

 

What Are Math Heuristics?

Math heuristics are problem-solving techniques that guide students to approach questions systematically. These strategies are especially helpful when the solution is not immediately obvious.

The Ministry of Education (MOE) and the Singapore Mathematics Curriculum identify heuristics as a core component in the development of mathematical thinking.

Common Math Heuristics Taught in Primary Schools:

• Draw a diagram or model
• Look for patterns
• Act it out
• Make a systematic list
• Guess and check
• Work backwards
• Use before-after concept
• Restate the problem in another way
• Simplify the problem
• Assume a value

Examples of Math Heuristics in Action

1. Draw a Diagram or Model

What it involves:
This heuristic helps children visualise the relationships in a problem. Common tools include bar models, number lines, or simple diagrams.

Sample Question and Application of Heuristic:
An adult ticket costs $6 more than a child ticket. 2 adults and 3 children paid $82. What is the cost of a child’s ticket?

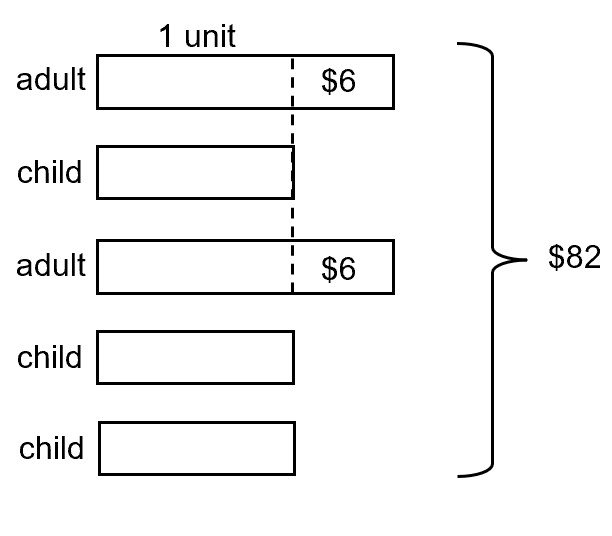
$6 × 2 = $12
$82 – $12 = $70
5 units = $70
1 unit = $70 ÷ 5 = $14 (ans)

 

2. Look for Patterns

What it involves:
This involves identifying repeated structures or trends to predict what comes next or to generalise a rule.

Sample Question and Application of Heuristic:
The first few terms of a number sequence is given by 5, 8, 11, 14, …
What is the 100^th term?

See that we need to add 3 to obtain the next term. Also we can rewrite the pattern into:

T₁ = 5
T₂ = 5 + 3
T₃ = 5 + 3 + 3
T₄ = 5 + 3 + 3 + 3

Pattern generalisation: To obtain the n^th term, we add (n − 1) number of threes to 5. For example, if we want to find the 20th number, we add 19 threes to 5.

T₁₀₀ = 5 + (100 − 1) × 3 = 302 (ans)

 

3. Act It Out

What it involves:
Students use physical actions or role-play to understand the steps and logic of a problem.

Sample Question and Application of Heuristic:
Ali has $24 more than Ben at first. Ben saves $4 every week, while Ali saves $1 every week. After some weeks, they both have the same amount of money. How many weeks does it take for their total amounts to be equal?

How to Act It Out:
• Use counters or notes to represent weekly savings.
• Represent Ali and Ben with labelled trays or boxes.
• Each week, add $4 to Ben and $1 to Ali.
• Continue until both trays show the same total.

The main objective here is to get students to understand that:
− Even though Ali has more money, eventually both boys will have the same amount of money because Ben saves more.
− The difference decreases by $3 with each passing week.
− The number of weeks required for both boys to have the same amount is given by
$24 ÷ $3 = 8 (ans)

 

4. Make a Systematic List

What it involves:
This helps organise all possible options or combinations in an orderly way to avoid missing any.

Sample Question and Application of Heuristic:
A fruit seller has some apples. If he packs 4 apples into a bag, he will have 2 apples left. If he packs 7 apples into a bag, he will be short of 2 apples. What is the smallest possible number of apples the fruit seller has?

By Listing Method, we have the following.

4 apples in a bag	7 apples in a bag
4 × 1 bag + 2 left over = 6 apples 4 × 2 bags + 2 left over = 10 apples 4 × 3 bags + 2 left over = 14 apples … 4 × 13 bags + 2 left over = 54 apples	7 × 1 bag – 2 short = 5 apples 7 × 2 bags – 2 short = 12 apples 7 × 3 bags – 2 short = 19 apples … 7 × 8 bags – 2 short = 54 apples

Ans: 54 apples

 

5. Guess and Check

What it involves:
Students make a reasonable guess, test it against the conditions, and adjust if needed. It builds estimation and reasoning skills.

Sample Question and Application of Heuristic:
The figure below is formed by two squares, P and Q. The length of each square is a whole number, and the total area of P and Q is 130 cm². What is the perimeter of the figure?

By visual inspection, the length of each square is likely to range from 6 cm to 11 cm.
Furthermore, the side of a square cannot be 12 cm since 12 × 12 = 144, which is greater than the given total area of 130 cm².

We will list the areas of squares with sides ranging from 6 cm to 11 cm.

6 × 6 = 36	9 × 9 = 81
7 × 7 = 49	10 × 10 = 100
8 × 8 = 64	11 × 11 = 121

Select two areas and check to see if they sum up to 130:
49 + 121 = 170 (✗)
49 + 81 = 130 (✓)

The length of the larger square is 9 cm and the length of the smaller square is 7 cm.

We can treat the figure as a 11 cm by 16 cm rectangle when calculating the perimeter. So the perimeter of the figure can later be calculated as
(11 + 16) × 2 = 54 cm (ans)

 

6. Work Backwards

What it involves:
Start from the final result and reverse the operations to find the starting value.

Sample Question and Application of Heuristic:
Peter had some money at first. He spent $12 on food and later received twice as much money as what he had left from his grandmother. Peter had $54 in the end. How much money did he have at first?

To apply Work Backwards, first make a simple diagram to represent what took place in chronological order. From the end, we gradually “fill in” information to obtain values at the earlier parts the diagram. In general, perform reverse operations when working backwards. For example, the reverse operation of multiplication is division and the reverse operation of subtraction is addition.

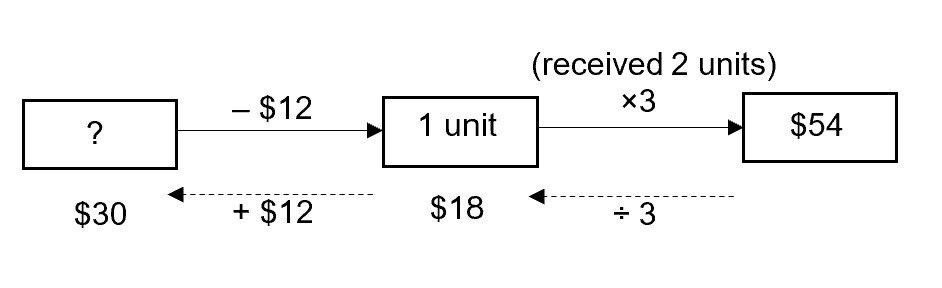
See that the final amount of $54 is made up of 3 units.

3 units = $54
1 unit = $54 ÷ 3 = $18
Amount at the start = $18 + $12 = $30 (ans)

 

7. Use Before-After Concept

What it involves:
This involves comparing a quantity before and after a change, often with bar models (or ratios) to show the difference or total. In many cases, we will need to look for what is changed and what remains unchanged (constant).

Sample Question and Application of Heuristic:
Mrs Goh is 45 years old and her nephew is 5 years old. In how many years’ time will Mrs Goh’s age be thrice her nephew’s age?

In the Before and After situations, students need to see that the age gap between any two persons will always be the same.

Age gap now between Mrs Goh and her nephew = 45 − 5 = 40 years

Future:

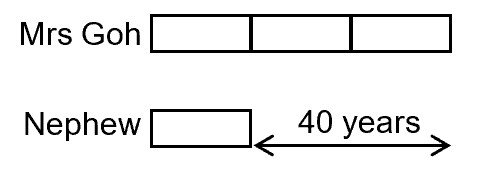
2 units = 40 yr
1 unit = 40 yr ÷ 2 = 20 yr

The nephew is 5 years old now. In the future, he will be 20 years old.
20 – 5 = 15 years’ time (ans)

 

8. Restate the Problem in Another Way

What it involves:
Rewriting the question in simpler or clearer terms helps in understanding what is being asked.

Sample Question and Application of Heuristic:
A packet of rice weighs 12 kg. Sally uses ⅕ of the packet of rice. How much rice is left? Express your answer in kilograms and grams.

This problem involves finding the leftover in fractions, which can confuse students. Restating it in simpler steps helps make the relationships clearer. This can also be done for students who prefer not to use the model method.

➡ Rephrase:
Instead of trying to process it all at once, rephrase it into parts:

1. “She uses ⅕ of the rice” → She has 4/5 of her rice left.
   Now the question becomes:
   What is ⅘ of 12 kg?
   5 units = 12 kg
   1 unit = 12 ÷ 5 = 2.4 kg
   4 units = 2.4 × 4 = 9.6kg = 9 kg 600 g (ans)

 

9. Simplify the Problem

What it involves:
Break a complex problem into simpler parts, or solve an easier version first.

Sample Question and Application of Heuristic:
A class of 40 students raised money for a charity event. Each student donated the same amount. Their total contribution was added the amount donated by the form and co−form teachers. The form and co−form teachers each donated $200. The total amount raised was $1560. What was the difference in amount donated by the form teacher and each student?

The question involves a combined total, but only part of it comes from students. To simplify, isolate the portion the students are responsible for before working out the individual amount.

How To Simplify the Problem:
1. Calculate the total amount donated by both teachers:
$200 × 2 = $400

2. Subtract the teacher contributions from the total amount raised:
$1560 − $400 = $1160

3. Divide by the number of students:
$1160 ÷ 40 = $29

4. Obtain difference:
$200 − $29 = $171 (ans)

 

10. Assumption

What it involves:
Temporarily assign a value to an unknown to test or simplify the problem.

Sample Question and Application of Heuristic:
There were 125 crystals to be used for making 25 pieces of necklaces and bracelets. A necklace will use up 8 crystals while a bracelet will use up 3 crystals. How many bracelets were made?

Assume all 25 pieces are necklaces. (Tip: always assume the item that is not required by the question)

Total no. of crystals to be used = 25 × 8 = 200

No. of crystals in excess = 200 – 125 = 75

To reduce the excess, we need to exchange some necklaces for bracelets.

When one necklace is removed, the total no. used crystals reduces by 8 and when replaced by one bracelet, the total no. of crystals used up will be increased by 3. So the overall reduction is 5.

Total no. of replacements = 75 ÷ 5 = 15
This means 15 necklaces are replaced by 15 bracelets.

So 15 bracelets were made. (ans)

How Polya’s Problem-Solving Approach is Used in Singapore Primary Maths

In Singapore primary schools, pupils are taught to solve word problems methodically, and this aligns very closely with George Polya’s Four-Step Problem Solving Process. Although teachers do not always refer to it by name, the underlying structure is the same.

1. Understand the Problem

Polya’s Step: Identify what is given, what is unknown, and what the question is asking.
In schools:
• Pupils highlight key information
• Teachers use guiding questions
• Bar models are used to visualise the relationships

2. Devise a Plan

Polya’s Step: Choose an appropriate method or strategy.
In schools:
• Pupils select suitable heuristics
• Teachers guide them to match strategies to problem types

3. Carry Out the Plan

Polya’s Step: Implement the strategy step by step.
In schools:
• Pupils show all working clearly
• Reasoning is explained verbally or in writing
• Pupils are encouraged to persist and stay systematic

4. Look Back and Check

Polya’s Step: Reflect on and evaluate the solution.
In schools:
• Pupils recheck their answers
• They substitute their answers back into the problem
• Self-checking and discussion are encouraged

How Can Parents Support at Home?

Here are some simple but powerful ways to help your child build heuristic skills and problem-solving confidence:

Create a Math-Friendly Environment

• Set aside 15-20 minutes daily for math discussion
• Have drawing materials ready for bar models
• Celebrate thinking process over correct answers

Ask the Right Questions

Instead of “What’s the answer?” try:

• “What do you notice about this problem?”
• “Which strategy might work here?”
• “Can you draw what’s happening?”
• “Does your answer make sense?”

Use Real Singapore Contexts

• Void deck playground sharing problems
• MRT travel time calculations
• Kopitiam food sharing scenarios
• Shopping at neighbourhood markets

Practice with P4-Appropriate Problems

• Keep numbers manageable (under 1000 for most problems)
• Use familiar contexts (school, home, Singapore places)
• Focus on one heuristic at a time initially
• Build complexity gradually

Tip for Parents: Polya’s 4-Step Guide at Home

If your child is stuck, guide them through these:

1. What is the problem asking? What do we know?
2. What method could you use? Have you encountered and solved similar problems before?
3. Try it out step by step.
4. Does your answer make sense?

In Summary

Primary 4 math heuristics are your child’s toolkit for mathematical success. These core strategies – drawing models, making tables, finding patterns, guessing and checking, working backwards, and making systematic lists – transform challenging problems into manageable steps.

Remember: the goal isn’t just getting correct answers, but developing logical thinking, building confidence, and creating independent problem-solvers ready for Singapore’s rigorous mathematics program.

Your support as a parent makes the crucial difference. By encouraging strategy use, celebrating thinking processes, and providing practice opportunities, you help your P4 child build the mathematical foundation essential for future academic success.

Together, we can raise problem solvers who are ready for the world.

Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later. 

This will be delivered to your email inbox.

 

 

Click here to download

Does your child need more help?

Find out more about our Math Tuition Class.

1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:

– Live Zoom lessons
– Adaptably, a smart learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital questions.
– 24/7 Homework Helper Service

We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.

We specialise in English, Math, Science, and Chinese subjects.

You can see our fees and schedules here >>

Primary Math Tuition

Secondary Math Tuition

 

2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses. This will help your child as they will go beyond simply practising with past exam papers and revise more effectively.

Your child can:

– Learn from recorded videos

– Get access to lots of common exam questions to ensure sufficient practice

– Get unlimited support and homework help

You can see the available courses here >>

Math Online Courses