Classroom Ready Decimals Worksheets and Guide
Singapore’s Primary 4 math curriculum covers fundamental decimal concepts, including place values, conversion between fractions and decimals, and performing basic operations with decimal numbers. Decimals form a critical foundation for numerical value calculations, measurements, and other advanced mathematical concepts in later years.
Our free Primary 4 Decimals Worksheets provide comprehensive practice for mastering the topic. Each concept explanation is followed by practice questions for your child. Answer keys are provided at the end for checking your child’s work.
Consider downloading these revision notes as a PDF for printing or reading. It will be delivered to your email inbox.

What is Decimal?
We have learnt in Primary 2 that numbers less than 1 can be expressed as fractions. An example of a fraction is 3/4.
Another way to represent parts of a whole is by using decimal values. Did you know, we started writing decimals when we learnt to count money in dollars and cents in Primary 2? Let’s recall.

See that the above represents a one−dollar coin, a twenty−cent coin and a five−cent coin. We write the total amount as $1.25 .
The number ‘1.25’ is a form of decimal, in which the dot (.) separates the whole from the parts. The number ‘1’ represents 1 whole (because we have one complete dollar) and the number ‘25’ represents 25 parts (because 100 cents make up one complete dollar and there are only 25 cents).
Money is one measurement that is often represented by decimals. Other measurements such as lengths, mass and volume can also be represented using decimals. See examples in the table below.
| Measurements | Example |
| Money | $1.25 |
| Length | 0.5 m |
| Mass | 1.2 kg |
| Volume | 3.05 ℓ |
Use this set of notes and worksheet to review the concepts of decimals.
You will learn the following decimals Concepts:
- Place and Value
- Comparing Decimals
- Ordering Decimals
- Expressing Decimals as Fractions
- Rounding Off Decimals
1. Decimals Up to 3 Decimal Places
(a) Various representations of decimals and place values (tenths, hundredths and thousandths)
Tenths
When 1 whole is divided into 10 equal parts, each part represents 1/10 or 0.1.
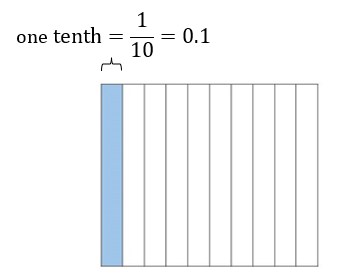
On a number line, tenths can be represented as follows:
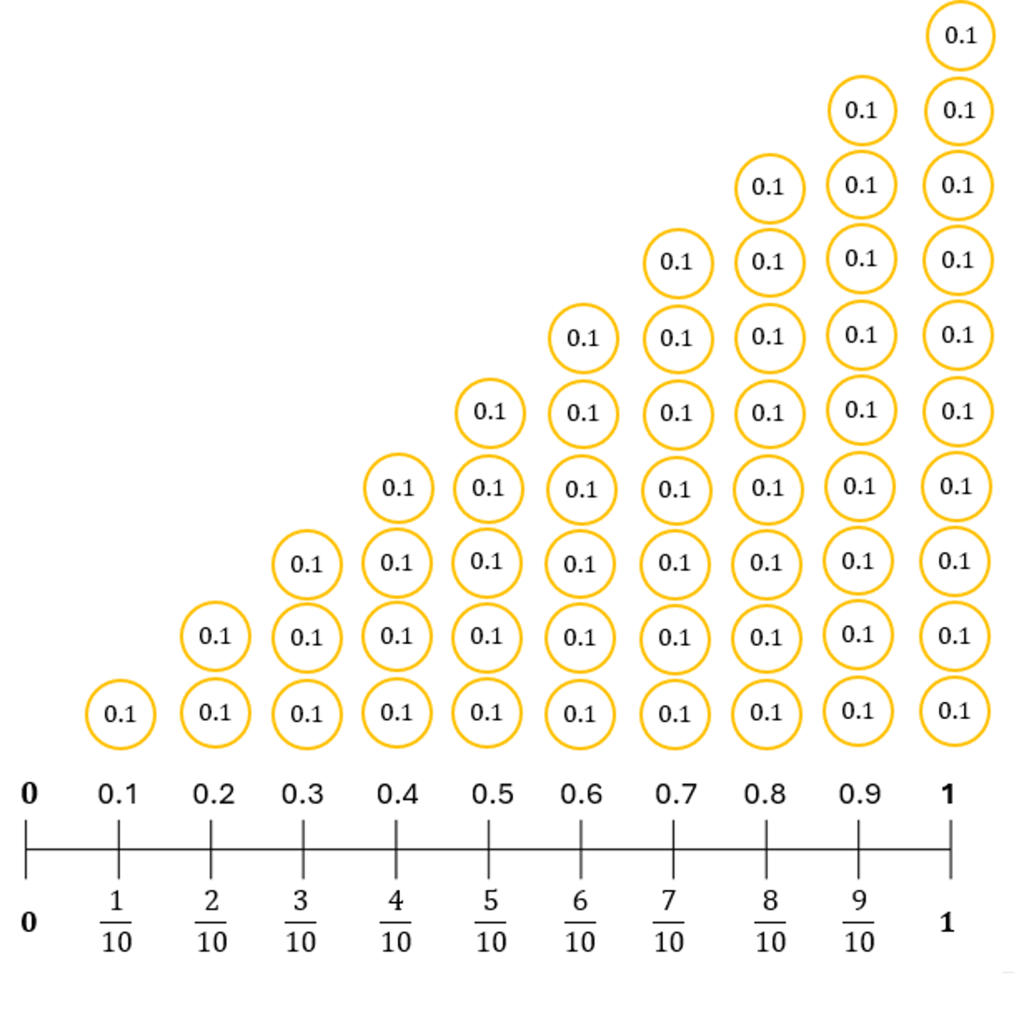
Important: 10 tenths make a whole.
Study the numbers below from 0 to 2. There are 10 equal intervals between each whole number. Therefore, each interval must represent an increment of 0.1 or one-tenth.

So (a) represents 0.3 and (b) represents 1.5.
In a place value table, tenths appear on the right side of ones as follows:
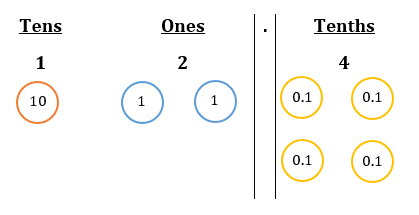
From the table: 10 + 2 + 0.4 = 12.4
The digit ‘1’ is in the tens place. It stands for 1 ten. Its value is 10.
The digit ‘2’ is in the ones place. It stands for 2 ones. Its value is 2.
The digit ‘4’ is in the tenths place. It stands for 4 tenths. Its value is 0.4.
Some examples of measurements involving the use of tenths.
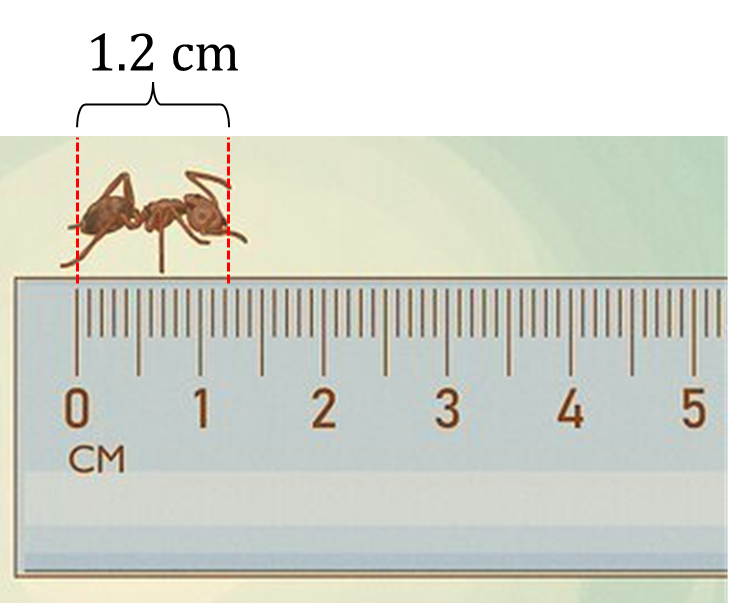
The length of the ant is 1.2 cm long.
*Use your ruler as a number line for counting in tenths!*

The total mass of the coffee powder and container is 10.3 g.

The bottle has a capacity of 1.5 ℓ.
Hundredths
When 1 whole is divided into 100 equal parts, each part represents 1/100 or 0.01.
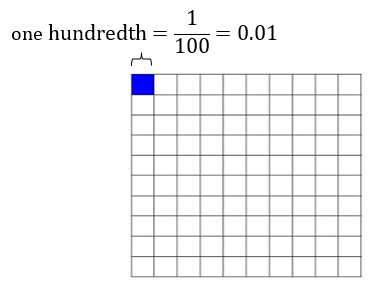
On a number line, tenths can be represented as follows:
Important: Ten hundredths make a tenth.
Study the number below from 0 to 0.2. There are 10 equal intervals between each tenth. Therefore each interval must represent an increment of 0.01 or one hundredth.

So (a) represents 0.02 and (b) represents 0.16.
In a place value table, hundredths appear on the right side of tenths as follows:
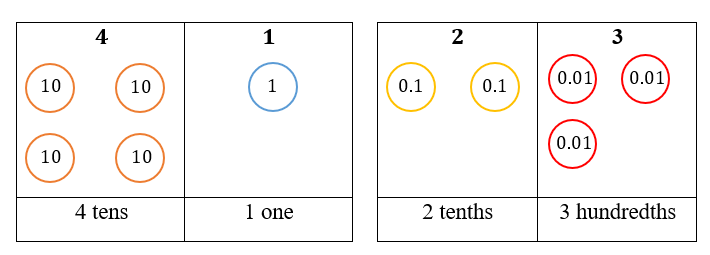
From the table: 40 + 1 + 0.2 + 0.03 = 41.23
The digit ‘4’ is in the tens place. It stands for 4 tens. Its value is 40.
The digit ‘1’ is in the ones place. It stands for 1 one. Its value is 1.
The digit ‘2’ is in the tenths place. It stands for 2 tenths. Its value is 0.2.
The digit ‘3’ is in the hundredths place. It stands for 3 hundredths. Its value is 0.03.
Some examples of measurements involving the use of hundredths.

The selling price of the item is $5.75.

The bathroom scale reads 46.66 kg.

The height of Bukit Timah Hill in Singapore is about 163.63m above sea level.
Thousandths
When 1 whole is divided into 1000 equal parts, each part represents 1/1000 or 0.001.
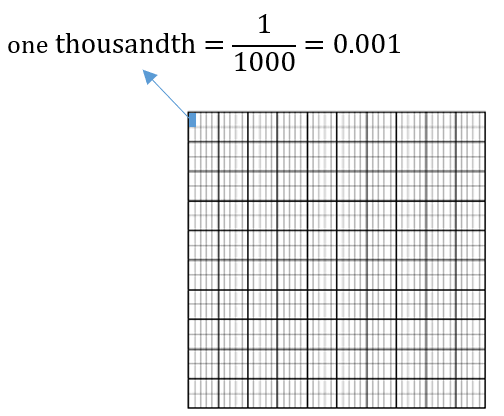
On a number line, thousandths can be represented as follows:
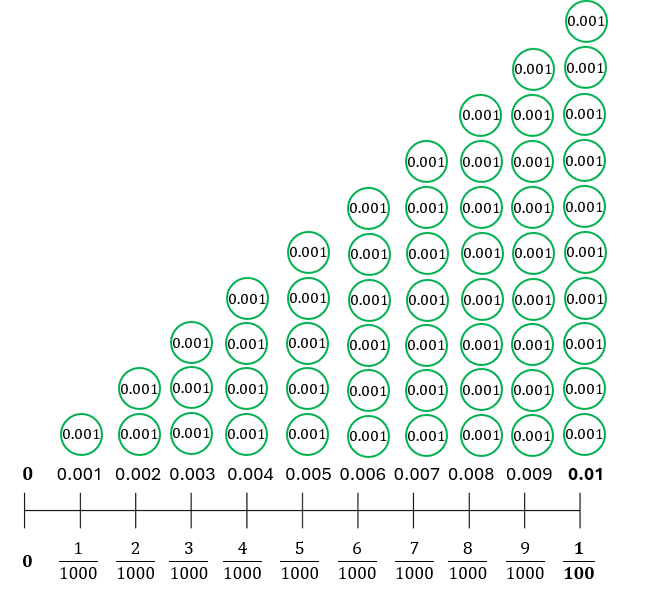
Important : Ten thousandths make a hundredth
Study the number below from 0 to 0.02. There are 10 equal intervals between each hundredth. Therefore, each interval must represent an increment of 0.001 or one thousandth.

So (a) represents 0.005 and (b) represents 0.019.
In a place value table, thousandths appear on the right side of hundredths as follows:
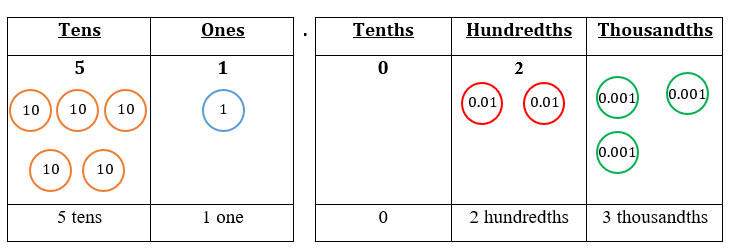
From the table: 50 + 1 + 0.0 + 0.02 + 0.003 = 51.023
The digit ‘5’ is in the tens place. It stands for 5 tens. Its value is 50.
The digit ‘1’ is in the ones place. It stands for 1 one. Its value is 1.
The digit ‘0’ is in the tenths place. It stands for 0 tenths. Its value is 0.
The digit ‘2’ is in the hundredths place. It stands for 2 hundredths. Its value is 0.02.
The digit ‘3’ is in the thousandths place. It stands for 3 thousandths. Its value is 0.003.
Some examples of measurements involving the use of thousandths.

Mount Everest, the tallest mountain the world stands at about 8.849 km above sea level.

A single raindrop holds about 1 ml of water. This is about 0.001 ℓ of water.
PRACTICE time!
Q1. Fill in the blanks.
(a) In 34.709, the value of the digit 7 is _____________.
(b) In 2.671, the digit 1 is in the _____________ place.
(c) 40 + 5 + 0.02 + 0.001 = _____________
(d) 2 + 11 tenths + 6 hundredths + 8 thousandths = _____________
Q2. State the decimal represented by the letter on each number line.
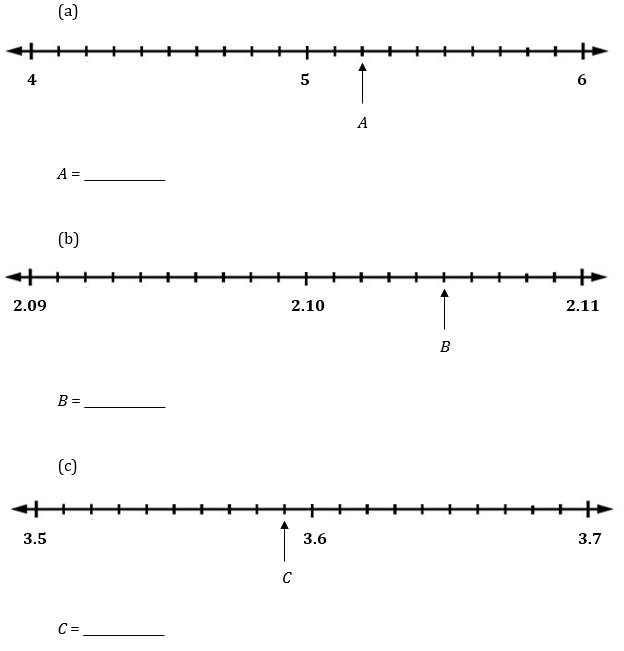
Answers:
Q1 (a) 0.7 (b) thousandths (c) 45.021 (d) 3.168
Q2 (a) 5.2 (b) 2.105 (c) 3.59
(b) Comparing and ordering decimals
Decimals appear very often in our everyday life, especially in areas where money and other measurements are involved. It is important we learn how to compare decimals effectively so that we can make smart and well−informed decisions.
Example
Arrange the following numbers in ascending order (from small to big).
3.65 , 3.6 , 3.605 , 4.0
Step 1: Line up the numbers. Write them one below the other, making sure the decimal points are lined up as follows. This allows you to compare digits with the same place values.
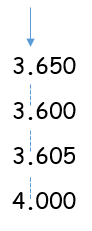
Step 2: Compare digit by digit, from the leftmost column.
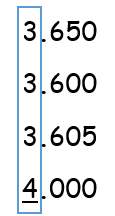
Observe that digit 4 is the largest in the ones place. Hence 4.0 is the largest among the given decimals. We can continue to compare the remaining three decimals.
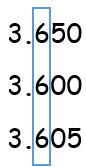
Observe that all the digits in the tenths placed are the same. We then move on to the hundredths place.
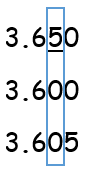
See that 3.650 has the largest digit in the hundredths place. So it is the second largest decimal. The remaining two decimals have the same digit in the hundredths place so we move on to compare the digits in the thousandths place.

See that 3.605 has the larger digit in the thousandths place. Hence 3.600 is the smallest decimal. We can now write the decimals in ascending order as follows:
Ans: 3.6 , 3.605 , 3.65 , 4.0
Tips to Remember
✅ Line up decimal points before comparing.
✅ Add extra zeros at the end if needed.
✅ Compare digits within same place, from left to right.
✅ The greater the number in the first different place, the bigger the decimal.
PRACTICE time!
Q1 Arrange the following numbers in ascending order.
5.79 , 5.907 , 5.097 , 5.9
Q2 Three decimals have been arranged in ascending order. The number that is in between 20.504 and 20.516 have some missing digits. The digits in the tens and thousandths places have been written. Identify the decimal in the middle.
20.504 , 2 __ . __ __ 0 , 20.516
Ans: _____________
Answers:
Q1 5.097 , 5.79 , 5.9 , 5.907
Q2 20.510
(c) Expressing decimals as fractions
Recall: one tenth = 0.1 = 1/10 and one hundredth = 0.01 = 1/100
Based on the above, we can easily express any decimal as a fraction.
Example
(a) Express 0.5 as a fraction in its simplest form.
*Recall: 0.5 is the same as 5 tenths.
0.5 = 5/10= 1/2 (Ans)
(b) Express 3.22 as a mixed number in its simplest form.
*Recall: 3.22 is the same as 3 wholes and 22 hundredths.
3.22 = 3 22/100 = 3 11/50 (Ans)
PRACTICE time!
Q1 Express the following decimals as fractions in the simplest form.
(a) 0.8 = __________ (b) 0.45 = __________
Q2 Express the following decimals as mixed numbers in the simplest form.
(a) 5.2 = __________ (b) 10.24 = __________
Answers:
Q1(a) 4/5 (b) 9/20
Q2(a) 5 1/5 (b) 10 6/25
(d) Expressing fractions with denominator 10 or 100 as decimals
Recall: one tenth = 1/10 = 0.1 and one hundredth = 1/100 = 0.01
Based on the above, we can easily express any fraction with denominator 10 or 100 as decimals.
Useful to memorise:
10 = 2 × 5 100 = 2 × 50 1000 = 8 × 125
= 4 × 25
= 5 × 20
Example
(a) Express 1/2 as a decimal
* Recall: 2 × 5 = 10
1/2 = 5/10 = 0.5 (Ans)
(b) Express 3/4 as a decimal
* Recall: 4 × 25 = 100
3/4 = 75/100 = 0.75 (Ans)
PRACTICE time!
Q1 Express the following fractions as decimals.
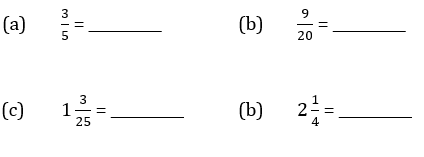
Answers:
Q1(a) 0.6 (b) 0.45 (c) 1.12 (d) 2.25
(e) Rounding decimals to either the nearest whole number, 1 decimal place or 2 decimal places
Rounding decimals means adjusting a decimal number to a simpler or more convenient value while keeping it as close as possible to the original number. This helps in estimating answers and measurements. It also makes calculations easier as there are less digits to handle.
Rounding decimals follows the same basic rules as rounding whole numbers, but instead of focusing on the ones, tens, or hundreds place, we look at tenths, hundredths, or thousandths place.
Rounding to the nearest whole number
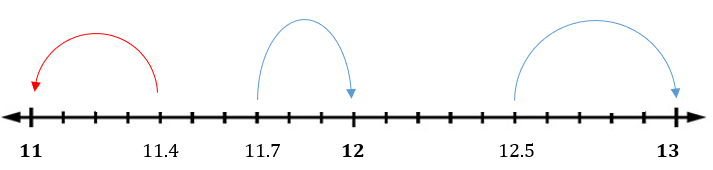
The number line below shows whole numbers from 11 to 13. The decimals 11.4, 11.7 and 12.5 are also shown on the number line.
See that:
− 11.4 is closer to 11 than 12. So 11.4 is 11 when rounded to the nearest whole number. We write 11.4 ≈ 11.
− 11.7 is closer to 11 than 12. So 11.7 is 12 when rounded to the nearest whole number. We write 11.7 ≈ 12.
− 12.5 is the centre of 12 and 13. So 12.5 is 13 when rounded to the nearest whole number. We write 12.5 ≈ 13.
Note that if the rounded value is smaller than the original value, then the number has been rounded down. So 11.4 has been rounded down to 11.
If the rounded value is greater than the original value, then the number has been rounded up. So 11.7 has been rounded up to 12, and 12.5 has been rounded up to 13.
Rounding to 1 decimal place
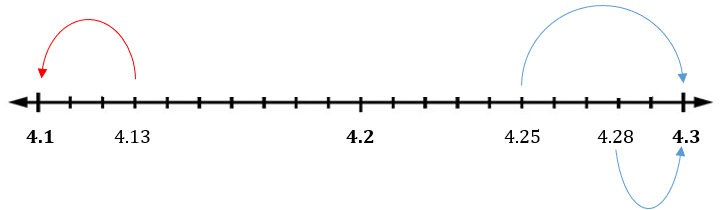
The number line below shows decimals from 4.1 to 4.3. The decimals 4.13, 4.25 and 4.28 are also shown on the number line.
See that:
− 4.13 is closer to 4.1 than 4.2. So 4.13 is 4.1 when rounded to 1 decimal place. We write 4.13 ≈ 4.1.
− 4.25 is the centre of 4.2 and 4.3. So 4.25 is 4.3 when rounded to 1 decimal place. We write 4.25 ≈ 4.3.
− 4.28 is closer to 4.3 than 4.2. So 4.28 is 4.3 when rounded to 1 decimal place. We write 4.28 ≈ 4.3.
Important : Rounding to 1 decimal place is the same as rounding to the nearest tenth.
Rounding to 2 decimal places
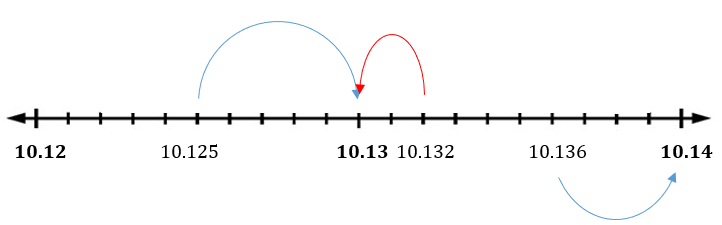
The number line below shows decimals from 10.12 to 10.14. The decimals 10.125, 10.132, and 10.136 are also shown on the number line.
See that:
− 10.125 is the centre of 10.12 and 10.13. So 10.125 is 10.13 when rounded to 2 decimal places. We write 10.125 ≈ 10.13.
− 10.132 is closer to 10.13 than 10.14. So 10.132 is 10.13 when rounded to 2 decimal places. We write 10.132 ≈ 10.13.
− 10.136 is closer to 10.14 than 10.13. So 10.136 is 10.14 when rounded to 2 decimal places. We write 10.136 ≈ 10.14.
Important : Rounding to 2 decimal places is the same as rounding to the nearest hundredth.
Rounding off without a number line
It may be time-consuming to construct a number line. Apply the following steps to round off numbers quickly and effectively.
Example 1
Round off 4.36 to the nearest whole number.
Step 1: Identify the digit in the place you are rounding off to. In the above example, we underline the digit 4.
4.36
Step 2: Highlight the digit to the right of the underlined digit. In the above example, we highlight the digit 3.
4.36
Step 3: Decide whether to round up or round down. If the circled number is less than 5, we round down. If the circled number is 5 or greater, then we round up. Since 3 is less than 5, we round down the decimal to the whole number 4. In the case where we need to round up, we add a one to the underlined place. Then the final answer will be 5 instead of 4. More on this later.
Step 4: Write out the rounded-off number. Ensure no digits are appearing after the underlined number.
4.36 ≈ 4 (ans)
Example 2
Round off 2.651 to the nearest tenth.
Step 1: Identify the digit in the place you are rounding off to. In the above example, we underline the digit 6.
2.651
Step 2: Highlight the digit to the right of the underlined digit. In the above example, we highlight the digit 5.
2.651
Step 3: Decide whether to round up or round down. Since 6 is more than 5, we shall round up by adding a one to the underlined tenths place (digit 6).
Step 4: Write out the rounded-off number. Ensure no digits are appearing after the underlined number.
2.651≈ 2.7 (ans)
Example 3
Round off 3.197 to 2 decimal places.
Step 1: Identify the digit in the place you are rounding off to. In the above example, we underline the digit 9.
3.197
Step 2: Highlight the digit to the right of the underlined digit. In the above example, we highlight the digit 7.
3.197
Step 3: Decide whether to round up or round down. Since 7 is more than 5, we shall round up by adding a one to the underlined hundredths place (digit 9). Note that 9 + 1 = 10. So the digit in the hundredths place is now 0, and we “carry” the 1 onto the digit 1 in the tenths place.
Step 4: Write out the rounded-off number. Ensure no digits are appearing after the underlined number.
3.197 ≈ 3.20 (ans)
Note that the digit 0 in the hundredths place must be written down since we are rounding off to two decimal places (or to the nearest hundredths). Writing 3.2 (instead of 3.20) will give a wrong answer even though 3.2 and 3.20 have the same value.
PRACTICE time!
Q1. Round off 3.458 to the nearest
(i) whole number,
(ii) tenth,
(iii) hundredth.
Ans: (i) _____________, (ii) _____________, (iii) _____________
Q2. Round off 10.982 to
(i) the nearest whole number,
(ii) 1 decimal place,
(iii) 2 decimal places.
Ans: (i) _____________, (ii) _____________, (iii) _____________
Answers:
Q1(a) 3 (b) 3.5 (c) 3.46
Q2(a) 11 (b) 11.0 (c) 10.98
2. Addition and Subtraction
(a) Addition and subtraction of decimals (up to 2 decimal places)
Performing addition or subtraction with decimals is just like adding or subtracting whole numbers, but you need to line up the decimal points properly during column addition or subtraction. Lining up the decimals ensures that all the digits are properly aligned in their correct places. Let’s review the steps:
Example 1
3.25 + 1.8 = _____________
Step 1: Carry out column addition, ensuring that decimal points are aligned.
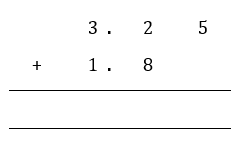
Step 2: Add up the digits starting from the rightmost column. You can write 1.8 as 1.80. If the sum of digits is more than 9, perform carry over as you would when adding whole numbers. Do not forget to add the decimal point in your answer.

3.25 + 1.8 = 5.05 (ans)
Example 2
3.25 − 1.8 = _____________
Step 1: Carry out column subtraction, ensuring that decimal points are aligned.
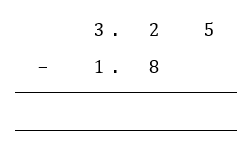
Step 2: Subtract the digits starting from the rightmost column. You can write 1.8 as 1.80. If the number on top is too small, “borrow” from the digit on the left as you would when subtracting whole numbers. Do not forget to add the decimal point in your answer.
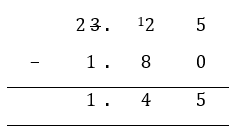
3.25 − 1.8 = 1.45 (ans)
Key Tips:
✅ Always line up decimal points before adding/subtracting.
✅ If a number has fewer decimal places, add extra zeros to make it equal.
✅ Add/subtract from right to left, just like whole numbers.
✅ Perform “carry over” or “borrowing” where necessary.
✅ Keep the decimal point in the same place in the answer.
PRACTICE time!
Q1 Find the sum of the following numbers.
(a) 5.2 + 4.36 = _____________
(b) 1.05 + 4.76 = _____________
(c) 8.99 + 3.02 = ____________
Q2 Find the difference between the following numbers.
(a) 8.51 – 4.4 = ____________
(b) 10.46 – 6.29 = _____________
(c) 19 – 7.28 = _____________
Answers:
Q1(a) 9.56 (b) 5.81 (c) 12.01
Q2 (a) 4.11 (b) 4.17 (c) 11.72
3 Multiplication and Division
(a) Multiplying and dividing decimals (up to 2 decimal places) by a 1−digit whole number
Multiplying decimals by a single-digit whole number is similar to column multiplication of whole numbers. The only difference is placing the decimal point correctly in the final answer. Let’s review the steps:
Example
4.72 × 3 = _____________
Step 1: Write out the column multiplication, with the single digit whole number in the second row.
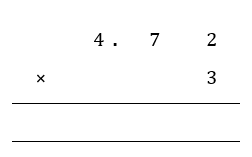
Step 2: Carry out column multiplication, multiplying the digit in the rightmost column with the whole number as you would when performing column multiplication with whole numbers. Carry over any excess digits. If there are two decimal places in the original decimal, then count two places from the right in your final answer and add in the decimal point.
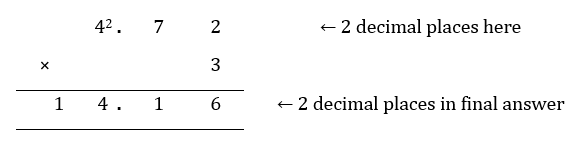
Ans: 4.72 × 3 = 14.16 (ans)
Dividing decimals by a single-digit whole number is similar to long division of whole numbers. The key difference is placing the decimal point correctly in the quotient (answer). Let’s review these steps:
Example 1
6.48 ÷ 3 = _____________
Step 1: Set up the long division frame.
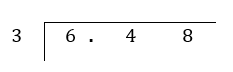
Step 2: Carry out long division as you would when dividing with whole numbers. Starting with the leftmost column, divide the number in the leftmost column by the divisor (in this case, 3). The decimal point in the quotient must be directly above the decimal point in the dividend.
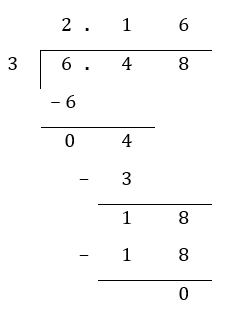
6.48 ÷ 3 = 2.16 (ans)
Example 2
1.68 ÷ 4 = _____________
Step 1: Set up the long division frame.
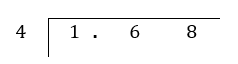
Step 2: Carry out long division as you would when dividing with whole numbers. Starting with the leftmost column, divide the number in the leftmost column with the divisor (in this case, 4). If the starting digit is not large enough to be divided by the divisor, put a 0 above the digit and use two digits instead. In the example below, when dividing by 4, we use 16 instead of 1.
The decimal point in the quotient must be directly above the decimal in the dividend.
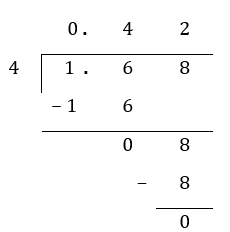
1.68 ÷ 4 = 0.42 (ans)
Example 3
6.42 ÷ 6 = _____________
Step 1: Set up the long division frame.
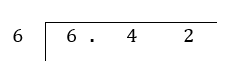
Step 2: Carry out long division as you would when dividing with whole numbers. Starting with the leftmost column, divide the number in the leftmost column by the divisor (in this case, 4). If the number is not large enough to divide by the divisor, put a 0 in the quotient and carry down the next number. In the example below, 4 is not large enough to be divided by 6. Here, we put a 0 in the quotient and bring down the digit 2. Then we use 42 instead of 4 to be divided by 6.
The decimal point in the quotient must be directly above the decimal point in the dividend.
6.42 ÷ 6 = 1.07 (ans)
PRACTICE time!
Evaluate the following.
(a) 4.36 × 5 = _____________
(b) 9.64 ÷ 4 = ____________
(c) 42.49 ÷ 7 = ____________
Answers
(a) 21.8 (or 21.80) (b) 2.41 (c) 6.07
(b) Dividing a whole number by a whole number with quotient as a decimal
When we divide 13 objects into 4 groups, we get a quotient of 3 and a remainder of 1.
13 ÷ 4 = 3 R 1
This means that each group has 3 objects, and there is a leftover of 1 object.
However, now that we have learnt decimals, we can treat the remainder of 1 whole as 10 tenths and continue to divide the remaining 10 tenths into 4 groups.
Let’s review the steps:
Example 1
Express 13 ÷ 4 as a decimal.
Step 1: Write out the long division frame and perform long division as usual.
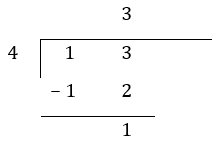
Step 2: When we decide to divide the remainder into smaller parts, add a decimal point and a 0 at the end of the dividend (in this case, 13). Then we bring down the digit 0 to combine it with the remainder (in this case, 1).
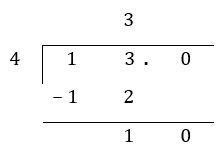
Step 3: We then carry out division as how we have done in the previous examples of division involving decimals. Observe that there is a remainder of 2 tenths.
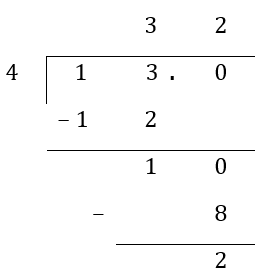
Step 4: We will proceed to add another 0 at the end of the dividend (in this case, the dividend is now 13.00). Bring down the last 0 to combine it with the remainder (in this case, 2) and continue to divide. Repeat until we have no more remainder of any parts. The decimal point in the quotient must be directly above the decimal point in the dividend.

13 ÷ 4 = 3.25 (ans)
Example 2
Divide 1 by 8.
Step 1: Write out the long division frame. If the starting digit is not large enough, we put a decimal dot and 0 at the end of the dividend (in this case, 1) and use 10 instead of 1. We also must put a 0 at the quotient t to indicate there are no wholes.

Step 2: Now carry out long division and continue to add zeroes to the dividend where necessary to divide until there is no remainder. The decimal point in the quotient must be directly above the decimal point in the dividend.

1 ÷ 8 = 0.125 (ans)
PRACTICE time!
Evaluate the following.
(a) 3 ÷ 4 = _____________
(b) 15 ÷ 8 = _____________
Answers
(a) 0.75 (b) 1.857
(c) Rounding quotients to a specified degree of accuracy
It is not always the case that all numbers can be divided until no remainder is left.
For example, when we divide 2 by 7, we get the following:
2 ÷ 7 = 0.285714285 …
The decimals go on and on indefinitely. In this case, we will have to round off the quotient to a certain number of decimal places.
Example 1
Divide 11 by 7, express your answer correct to 1 decimal place.
Step 1: Carry out long division as usual, applying all the steps as we have reviewed previously. Since the question requires an accuracy up to 1 decimal place, we will stop long division when we have 2 decimal places in our quotient. There is no need to obtain any more digits in our quotient since we only require 2 decimal places for rounding off answers to 1 decimal place.
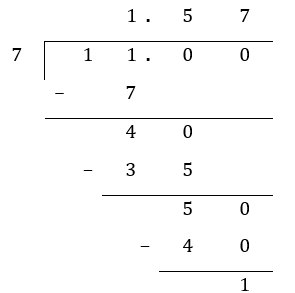
Step 2: Once we have 2 decimal places, we can decide to round up or down with the last digit. In the example above, we will round up (since 7 is greater than or equal to 5).
11 ÷ 7 ≈ 1.6 (ans)
Note the use of the approximate sign, instead of ‘=’. It is inaccurate to write 11 ÷ 7 = 1.6.
Example 2
Divide 15 by 9, express your answer correctly to 2 decimal places.
Step 1: Carry out long division as usual, applying all the steps as we have reviewed previously. Since the question requires an accuracy up to 1 decimal place, we will stop long division when we have 3 decimal places in our quotient. There is no need to obtain any more digits in our quotient since we only require 3 decimal places for rounding off answers to 2 decimal places.
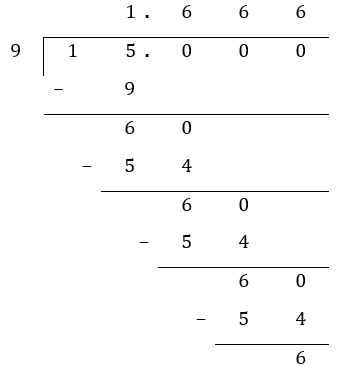
Step 2: Once we have 3 decimal places, we can decide to round up or down with the last digit. In the example above, we will round up (since 6 is greater than or equal to 5).
15 ÷ 9 ≈ 1.67 (ans)
Note the use of the approximate sign, instead of ‘=’. It is inaccurate to write 15 ÷ 9 = 1.67 (ans)
PRACTICE time!
(a) Divide 21 by 8, expressing your answer correct to the nearest whole number.
(b) Divide 4 by 9, expressing your answer correct to the nearest tenth.
(c) Divide 22 by 7, expressing your answer correct to 2 decimal places.
Answers:
(a) 3 (b) 0.4 (c) 3.14
Need More Revision Notes for Primary School Math?
Check out our exam guide on other topics here!
Consider downloading these revision notes as a PDF for printing or reading. The digital file will be sent to your email inbox.

Does your child need help with Mathematics?
1) Live Zoom Math Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:
– Live Zoom lessons
– Adaptably™, an AI-powered learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital worksheets.
– 24/7 Homework Helper Service
We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.
We specialise in English, Math, Science, and Chinese subjects.
View our fees and schedules:
2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child to learn at his or her own pace, you can join our pre-recorded online Math courses.
Learn Math Effectively with:
– Recorded videos
– Access to math resources and exam questions for sufficient practice
– Unlimited support and homework help
Browse our available courses here:
