In probability theory, it is crucial to distinguish between mutually exclusive events and independent events. Mutually exclusive events cannot occur simultaneously; the occurrence of one event precludes the occurrence of the other. On the other hand, independent events are those where the occurrence of one event does not affect the probability of the other event occurring.
Grasping these concepts is essential for accurately analysing and calculating probabilities in various scenarios. For a more detailed explanation and examples, please refer to the information provided below.
Before you read on, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.
Mutually Exclusive Events, also called disjoint events, are a part of probability theory that describe events that invalidate one another.
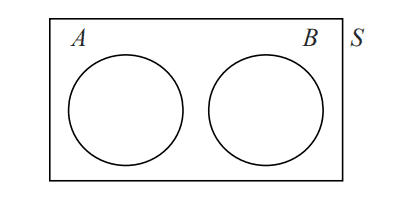
If two sets of events (A and B) cannot occur at the same time, then they are two mutually exclusive events. For example, when tossing a coin, event A: ‘Heads’ and event B: ‘Tails’ are mutually exclusive events, as the coin can only come up as either a head or a tail.
|
In general,
|
A fair die is tossed. Find the probability of obtaining
i) either 1 or 4; ii) neither 1 nor 4; iii) 1 and 4.
Solution
i) A dice cannot show both 1 or 4 at the same time so obtaining 1 and obtaining 4 from a die throw are mutually exclusive events. A dice roll has a 1/6 chance of landing on each face.
P(1 or 4) = P(1) + P(4)
= 1/6 + 1/6
= 1/3
ii) P(neither 1 nor 4) = 1 – P(1 or 4)
= 1 – 1/3
= 2/3
iii) There is only one number on each face of a die so this is an impossible outcome and event.
P(1 and 4) = 0
A fair 6-sided die is tossed. Given event A: ‘rolling an even number’ and event B: ‘rolling a prime number’, find P(A ∪ B).
Solution
Events A and B are not mutually exclusive because the number shown on the dice can be both even and prime at the same time. To find P(A ∪ B), we need to consider the elements of A ∩ B to avoid double counting.
A = {2, 4, 6}
B = {2, 3, 5}
A ∩ B = {2}
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 1/2 + 1/2 – 1/6
= 5/6
If two events A and B are independent, the occurrence or non-occurrence of A does not affect the probability of B occurring or not occurring.
Examples of Independent Events
1. event A: ‘picking a Queen from a deck of cards’ and event B: ‘getting a tail from a coin toss’.
2. randomly picking a Queen from a deck of cards, replacing it and then picking a King from the same deck
Mutually exclusive events cannot be independent events.
For example, if you toss a coin and get a ‘Heads’, you cannot at the same time get a ‘Tails’, and vice-versa. In this way, both events are always dependent on each other.
If the occurrence or non-occurrence of A affects the probability of B occurring or not occurring, then the two events are dependent.
For example, randomly picking a Queen from a deck of cards, and then picking a King from the same deck.
Dependent events may or may not be mutually exclusive events.
– Dependent and NOT Mutually Exclusive – Consider the event A: ‘there is a traffic jam on a rainy Wednesday morning’ and event B: ‘you are late for school’. Event B is not independent of A since there is a higher chance of being late when the traffic is bad. Both events are not mutually exclusive because they can occur at the same time i.e. there is a traffic jam on a rainy Wednesday morning AND you are late for school.
– Dependent and Mutually Exclusive – Consider the event A: ‘you make it in time for school’ and event B: ‘you are late for school’. Event B is not independent of A since there is a zero chance of being late when you make it in time for school. Hence, the existence of event B depends on the non-existence of event A. Moreover, both events are mutually exclusive because one cannot be both on time and late at the same instance!
As a result, it is not possible to draw Independent Events on a Venn Diagram because the two or more events may or may not overlap each other. We usually use a Probability Tree Diagram instead, to display all the possibilities of events that do not affect one another.
|
In general,
|
Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.
At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:
– Live Zoom lessons
– EdaptIQ™, a smart learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital worksheets.
– 24/7 Homework Helper Service
We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities. We also offer a free trial class and consultation with our tutors, to help make sure we are the best fit for your child.
We specialise in English, Math, and Science subjects.
You can see our fees and schedules here >>
If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.
Your child can:
– Learn from recorded videos
– Get access to lots of common exam questions to ensure sufficient practice
– Get unlimited support and homework help
You can see the available courses here >>
