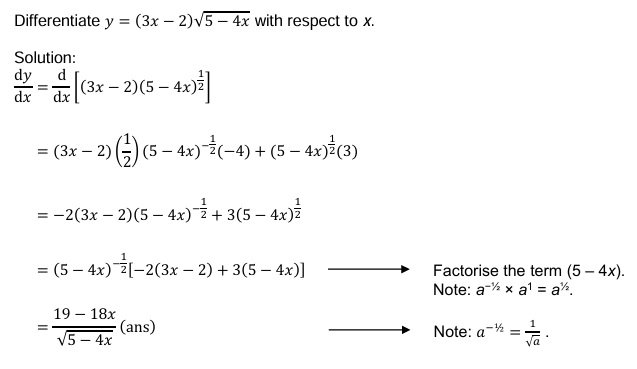Introduction to Differentiation: Maths Exam Guide

The Big Idea of Differentiation

Differentiation is one of the most exciting and powerful tools in mathematics. It helps us understand and describe how things change.

Imagine you are cycling uphill, and you want to know how steep the hill is at a specific point.

Or think about how fast a rocket is speeding up as it soars into the sky.

Differentiation gives us the mathematical language and techniques to answer questions like these.

At its heart, differentiation is about rates of change.

A rate of change tells us how one quantity changes when another quantity changes.

For example, when we talk about the speed of a car, we are describing how the car’s position changes over time. Differentiation lets us calculate that speed precisely.

Even more, differentiation is not limited to physical movement. It can be used to study how populations grow, how temperatures change, or even how the brightness of a star varies. It allows us to take complex, real-world problems and break them down into manageable pieces.

Before you read on, you might want to download this entire revision notes in PDF format to print it out, or to read it later.

This will be delivered to your email inbox.

 

Click here to download

Why Study Differentiation?

At the secondary school level, learning differentiation serves as an essential foundation for understanding change and motion in both mathematics and real−world applications. The primary purposes include:

1. Building Critical Thinking Skills: Differentiation encourages students to think critically about relationships between variables and how quantities change, fostering problem-solving abilities.

2. Preparing for Advanced Mathematics: Differentiation is a core concept in calculus, which is a gateway to advanced studies in mathematics, physics, engineering, and economics.

3. Real-World Applications: It helps students solve practical problems, such as calculating speed, optimising costs, and understanding growth rates, which are directly applicable in various fields.

4. Enhancing Graphical Understanding: Differentiation aids in analysing graphs, such as determining slopes, identifying turning points, and understanding trends.

5. Laying Foundations for Science and Technology: Concepts from differentiation are critical in physics for understanding motion (velocity and acceleration), and in economics for marginal analysis.

By learning differentiation, you will gain a powerful mathematical tool that supports both academic growth and practical problem-solving in everyday life. This guide will introduce you to the basics of differentiation, covering the following key areas:

− The Derivative of a Function

− Basic Techniques of Differentiation

− Common Mistakes When Applying Differentiation Techniques

The Derivative of a Function

In mathematical terms, differentiation is the process of finding a derivative. A derivative measures the rate of change of a function at a specific point. You can think of it as finding the slope (or gradient) of a curve. 

Here are some important terms you need to know:

1. Function: A mathematical rule that connects two variables, usually x and y, in the form y = f(x). For example, y = x². You can also think of a function such that an input of x gives an output of y. When we input x = 3 into y = x², we get an output of y = 3² = 9.
2. Gradient: The slope (or steepness) of a line or curve at a particular point.
3. Derivative: The rate of change of y with respect to x.
4. The notation dy/dx represents the derivative of y with respect to x. If y = f(x), then the derivative may also be denoted by f ‘ (x) [usually read as f prime x]. f ‘ (x) is also known as the gradient function of a curve, that tells you the gradient of the curve at a particular point on the curve.

Note that the notation dy/dx is not a fraction, although the value of dy/dx can be a fraction.

5. The process of obtaining dy/dx of a given function is called differentiation. The differentiation process will involve application of various techniques to the given algebraic equation (which we will cover later on in this article).

How to Obtain the Gradient of a Curve

The gradient of a curve is not fixed unlike the gradient of a straight line.

To obtain the gradient of the curve at a specific point, we draw a tangent to the curve at that specific point, then calculate the gradient of the tangent since the gradient of the tangent and gradient of the curve at the same point are equal.

However, this method is:

− firstly, time consuming because both the curve and tangent needs to be drawn, and

− secondly, the derived gradient value can also be inaccurate because visual estimation is greatly involved in the process of drawing the curve and tangent line.

When we obtain the derivative of the function by differentiation, we will be able to conveniently obtain the gradient of the curve at any specific valid point without drawing any tangent.

Example of using differentiation to obtain the gradient of a curve

Given the function y = x². Applying relevant differentiation techniques (more on techniques in later part of this article), we obtain the derivative, dy/dx = 2x.

This means that when we want to find the value of the gradient of the curve, y = x², say at x = 5, we substitute x = 5 into the derivative and obtain dy/dx = 10.

Hence the gradient of the curve y = x², at x = 5, is 10.

This is much more efficient than having to draw the curve and its respective tangent at x = 5.

Summary of obtaining the gradient of a curve:

Differentiation Techniques

Historically, mathematicians obtain derivatives of various functions based on the method of differentiation by First Principles.

\[f'(x) = \lim_{h \to 0} \frac{f(x+h) – f(x)}{h}\]

However, the method of differentiation by First Principles itself is also a lengthy and complicated process. Thankfully, mathematicians developed some rules and techniques over the years that we can now use conveniently!

The sections below cover the common rules and techniques that you are required to learn and apply for the O levels.

 

Power Rule

If y = xⁿ , where n is a rational number, then

\[\frac{dy}{dx} = \frac{d}{dx}(x^n) = nx^{n-1}\]

More specifically, when the power of x = 0 (that is the term is a constant term), then the differentiation of a constant c will always result in a value of 0.

This is because when given y = c, then y = c is a horizontal line on the cartesian plane, and the gradient of any horizontal line is 0.

Also when we apply the Power Rule:

\[y = c = c x^0\]

Then

\[\frac{dy}{dx} = \frac{d}{dx}(c x^0) = (0)(c)x^{0-1} = 0. \]

(Multiplication with 0 gives a product of 0)}.

Example of Power Rule

Find the derivative of  \[\frac{1}{\sqrt[2]{x^3}}.\]

Solution:
\[\frac{d}{dx} \left( \frac{1}{\sqrt[2]{x^3}} \right) = \frac{d}{dx} \left( x^{-\frac{3}{2}} \right) \\
= \left( -\frac{3}{2} \right) x^{-\frac{3}{2} – 1} \\
= \left( -\frac{3}{2} \right) x^{-\frac{5}{2}} \\
= -\frac{3}{2 \sqrt[2]{x^5}} \]

Constant Multiple Rule

(i) If we have kf(x) and k is a constant, then

\[\frac{d}{dx} \left[ kf(x) \right] = k \frac{d}{dx} \left[ f(x) \right] = kf'(x).\]

(ii) Also if y = kxⁿ and k is a constant, then

\[\frac{dy}{dx} = \frac{d}{dx} \left( kx^n \right) = k \frac{d}{dx} \left( x^n \right) = knx^{n-1}.\]

Example of Constant Multiple Rule

Find \[\frac{dy}{dx} \text{ for } y = -3x^4. \]

Solution:
\[\frac{dy}{dx} = -3 \frac{d}{dx} \left( x^4 \right) \\
= -3 (4)(x^3) \\
= -12x^3 \]

Sum and Difference Rule

The Sum and Difference Rule allows us to differentiate expressions such as \[5x^2 – 3x + 7 \]

Given the expression \[f(x) \pm g(x),\]
\[\frac{d}{dx} \left[ f(x) \pm g(x) \right] = \frac{d}{dx} f(x) \pm \frac{d}{dx} g(x) = f'(x) \pm g'(x).\]

Example

Find \[\frac{dy}{dx} \text{ for } y = 5x^2 – 3x + 7.\]

Solution:
\[\frac{dy}{dx} = \frac{d}{dx} \left( 5x^2 \right) – \frac{d}{dx} \left( 3x \right) + \frac{d}{dx} \left( 7 \right) \\
= 5(2)x – 3 + 0 \\
= 10x – 3 \]

Chain Rule (for composite functions)

If y = f[g(x)], then
\[\frac{dy}{dx} = f'[g(x)] \times g'(x).\]

Example of Chain Rule

If \[y = (x^2 – 3x – 4)^5,\] find dy/dx.

Solution:
\[\frac{dy}{dx} = 5(x^2 – 3x – 4)^4 \times \frac{d}{dx}(x^2 – 3x – 4) \\
= 5(x^2 – 3x – 4)^4 (2x – 3)\]

Product Rule

Given a product of 2 functions in x, f(x)g(x), then
\[\frac{d}{dx} \left[ f(x)g(x) \right] = f(x)g'(x) + g(x)f'(x).\]

Caution:** Do not apply the distributive law!

\[\frac{d}{dx} \left[ f(x)g(x) \right] \neq \frac{d}{dx} \left[ f(x) \right] \times \frac{d}{dx} \left[ g(x) \right].\]

Example of Product Rule

Quotient Rule

Given a fraction of 2 functions in x, f(x)/g(x),
\[\frac{d}{dx} \left[ \frac{f(x)}{g(x)} \right] = \frac{g(x)f'(x) – f(x)g'(x)}{[g(x)]^2}.\]

**Caution:** Do not apply the distributive law!
\[\frac{d}{dx} \left[ \frac{f(x)}{g(x)} \right] \neq \frac{d}{dx} \left[ f(x) \right] \div \frac{d}{dx} \left[ g(x) \right].\]

Example of Quotient Rule

Common Mistakes When Applying Differentiation Techniques

When learning differentiation, it is normal to make mistakes, especially as you start applying different rules. Understanding these common errors and how to avoid them can save time and frustration. Here are some common mistakes, along with examples and tips to help you succeed.

1. Forgetting the Power Rule’s Adjustment 

Mistake: Students often forget to reduce the power by one after multiplying by the power (or index).

Example:

f(x) = x⁴ , Incorrect: f′(x)= 4x⁴

Correct:

f′(x) = 4x³

Tip: Always remind yourself that differentiation reduces the power by 1. Write down each step to avoid missing this adjustment.

2. Misusing the Product Rule 

Mistake: Applying the product rule incorrectly by neglecting one of the terms or mixing up the derivatives. 

Example:

f(x)=(x²)(x + 1), Incorrect: f′(x)=(2x)(x + 1) [Sum and Difference Rule wrongly applied here]

Correct (Product Rule):

\[f'(x) = (x^2) \frac{d}{dx} \left( x+1 \right) + (x+1) \frac{d}{dx} \left( x^2 \right) \\
= (x^2)(1) + (x+1)(2x) \\
= 3x^2\]

Tip: Determine the term to “keep” and the term to differentiate first then switch them around. Another simple way to remember the Product Rule is to use this version of the formula:

\[\frac{d}{dx}(uv) = uv’ + vu’\]

3. Ignoring the Chain Rule 

Mistake: Forgetting to differentiate the inner function when dealing with composite functions. 

Example:

f(x)=(2x + 3)⁴ , Incorrect: f′(x) = 4(2x+3)³

Correct:

\[f'(x) = 4(2x + 3)^3 \left[ \frac{d}{dx}(2x + 3) \right] \\
= 4(2x + 3)^3 (2) \\
= 8(2x + 3)^3\]

Tip: Always check if there is an “inner function” (something inside brackets or another function). Apply the chain rule whenever a composite function is present.

4. Misapplying the Quotient Rule 

Mistake: Swapping terms in the numerator or forgetting to square the denominator or using addition in the numerator.

Example:
\[f(x) = \frac{x^2}{x+1},\]

incorrect: \[f'(x) = \frac{(x+1)(2x) + (x^2)(1)}{x+1}\]
The sign in the middle should be a subtraction and denominator should be squared,

Correct (Quotient Rule):
\[f'(x) = \frac{(x+1)\left[ \frac{d}{dx}(x^2) \right] – (x^2)\left[ \frac{d}{dx}(x+1) \right]}{(x+1)^2} \\
= \frac{(x+1)(2x) – (x^2)(1)}{(x+1)^2} \\
= \frac{(x+1)(2x) – (x^2)}{(x+1)^2} \\
= \frac{x(3x+2)}{(x+1)^2}.\]

Tip: Write the quotient rule formula clearly:

Double−check that the denominator is squared and determine the term to “keep” and the term to differentiate first then switch them around.

5. Forgetting to Differentiate Constants 

Mistake: Treating constants as variables or failing to include them in the differentiation.

Example:

f(x)=3x² + 5, Incorrect: f′(x) = 6x + 5 [did not differentiate constant]

Correct:

f′(x) = 6x 

Tip: Apply the Sum and Difference Rule and double−check it is applied properly.

6. Overlooking Negative Signs 

Mistake: Dropping (or forgetting) negative signs during differentiation.

Example:

f(x) = −x⁻³ , Incorrect: f′(x) = −3x⁻⁴, Incorrect: f′(x) = 3x⁴

Correct:

f′(x) = −(−3)x⁻³⁻¹ = 3x⁻⁴

Tip: Keep an eye on signs at every step. It can help to circle negative signs (in pencil) when you spot them, ensuring they are included in your final result. Also note that the product of two negative terms will yield a positive term.

7. Failing to Simplify Expressions 

Mistake: Leaving derivatives in unnecessarily complicated forms. 

Example:

f(x) = (3x + 1)⁴, Incorrect: f′(x) = 4(3x + 1)³(3) [not simplified] 

Correct:

f′(x) = 4(3x + 1)³(3) = 12(3x + 1)³

Tip: After applying the differentiation rules, always simplify the final expression unless the question specifies otherwise. This ensures your answers are clear and concise. Also, factorising can also help, especially in the case when Power and Quotient Rules are applied. Refer to the examples in Power and Quotient Rules.

8. Applying the Wrong Rule

Mistake: Using the product rule when only one term is a function, or the chain rule when it is unnecessary. 

Example:

f(x) =x² + 3x , Incorrect: f′(x) =(x²)(3) + (3x)(2x)  [wrong application of Power Rule]

Correct:

f′(x) = 2x + 3

Tip: Before solving, take a moment to identify whether the function involves sums, products, quotients, or composites. This will guide you to the correct rule.

By being aware of these common mistakes and actively working to avoid them, you can develop confidence and accuracy in differentiation. Remember, practice and careful attention to detail are key!

Conclusion

Differentiation is an important maths skill that helps us understand how things change, like how fast a car is moving or how steep a hill is.

This guide explains the basics of differentiation, focusing on how to find a derivative function (the rate of change) and use it to solve problems. It covers useful techniques like the power rule, product rule, chain rule, and quotient rule, which make solving problems easier and faster.

The guide also highlights common mistakes students often make, like forgetting to reduce powers, mixing up rules, or skipping constants, and gives helpful tips to avoid these errors.

Learning differentiation will not only improve your problem-solving skills but also prepare you for more advanced topics in maths, science, and other subjects.

With practice and attention to detail, you can confidently tackle differentiation problems and use it to explore the world around you.