How to Find Volume of Liquid in a Container

Before you read on, you might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.

This will be delivered to your email inbox.

1. Finding the volume of liquid in a rectangular tank

(a) Measurement units for volume and conversion

Measurement Units
The common measurement units used for volume are millilitres (ml), litres (ℓ), cubic centimetres (cm3) and cubic metres (m³).
*Other measurement units include ounces, pints and gallons. These units are more commonly use in America and are not tested in the PSLE syllabus.

Conversion of Units
1 cm³ = 1 ml
1 000 cm³ = 1 000 ml = 1 ℓ
1 000 ℓ = 1 m³
*Conversion between cm³ and m³ is not tested in PSLE syllabus

Examples

Practice

Complete the table for the conversion of units below.

Answer:

 

(b) Relationship between water level and proportion of tank that is filled

When we fill a tank with water, the water level shows how much space the water takes
up in the tank. The higher the water level, the more the tank is filled.

• If the water level is low, only a small part of the tank is filled.
• If the water level is halfway, the tank is half−full.
• If the water level is at the top, the tank is completely full.

This is called the proportion of the tank that is filled.

Example

The tank below measures 24 cm by 12 cm by 16 cm.

The tank below measures 25 cm by 10 cm by 15 cm.

Complete the table below to show how the water level relates to the proportion of tank

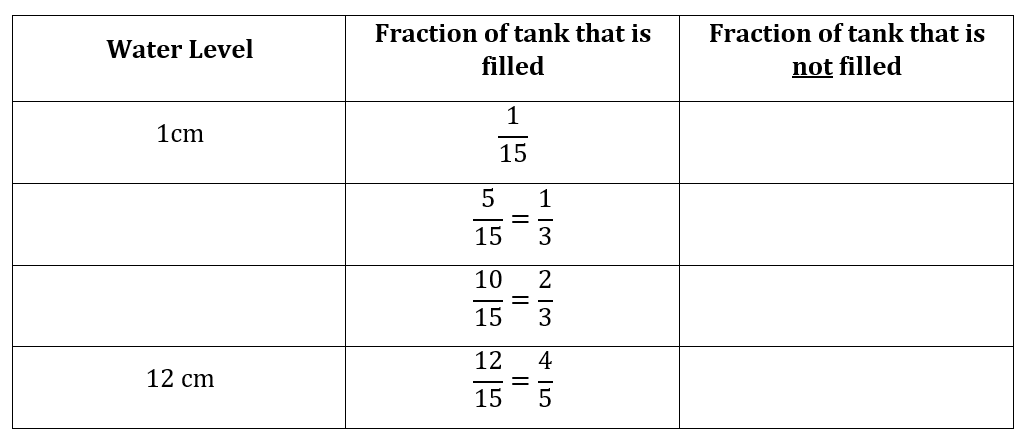
Answer:

 

(c) Finding the volume of liquid in a rectangular tank

− Using formula

Recall the formula:
Volume of a cuboid = Length × Breadth × Height

When water is poured into a rectangular tank, water takes up the shape of the tank, and
so water takes up the shape of a cuboid. Hence:
Volume of water in a rectangular tank = Length × Breadth × Water Level

Example
The tank below measures 24 cm by 12 cm by 16 cm.

If water is poured into the tank to a height of 5 cm, how much water is poured into the
tank?

Solution:
Volume of water = Length × Breadth × Water level
= 24 cm × 12 cm × 5 cm
= 1440 cm³ (ans)

Practice

The tank below measures 25 cm by 10 cm by 15 cm.

If water is poured into the tank to a height of 11 cm, how much water is poured into the
tank?

Solution:
Volume of water = Length × Breadth × Water level
= 25 cm × 10 cm × 11 cm
= 2750 cm³ (ans)

− Using base area and water level

Recall: Volume of liquid in a rectangular tank = Length × Breadth × Water level.

See that Length × Breadth = base area of the cuboid. And so this formula can be
shortened to:

Volume of liquid in a rectangular tank = Base Area of tank × Water level

Example

Water is poured into a tank up to a water level of 4 cm.

Given that the base area of the tank is 360 cm², how much water is poured into the tank?

Solution:
Volume of water = Base Area of tank × Water level
= 360 cm² × 4 cm
= 1440 cm³ (ans)

Practice

Water is poured into a tank up to a water level of 11 cm.

Given that the base area of the tank is 420 cm², how much more water is required to fill
the tank to its brim? Express your answer in litres.

Solution:
Height of unfilled space in tank = 20 – 11 = 9 cm
Volume of water required = Base Area of tank × Height of empty space
= 420 cm² × 9 cm
= 3780 cm³
= 3.78 ℓ (ans)

 

2. Finding the water level given the volume and base area

Recall the formula for area:
Area of a rectangle = Length × Breadth
If we are given the area of a rectangle and its length, then

Breath of rectangle = area of rectangle/length

Applying the above idea to:
Volume of liquid in a rectangular tank = Base Area of tank × Water level

The formula can be arranged into:

Water level = volume of liquid in a rectangular tank/Base Area of tank

Instead of finding the volume of water in a rectangular container, some questions require us to work backwards to find the water level. We will use the above formula to
calculate the water level.

Example
3 litres of water is poured into a tank as shown below.

Given that the base area of the tank is 250 cm², what is the water level in the tank?

Solution:
3 ℓ = 3000 cm³

Water level = volume of liquid in a rectangular tank/Base Area of tank

= 3000 cm³/250 cm³

= 12 cm (ans)

Practice

2 ℓ 750 ml of water is poured into a tank as shown below.

Given that the base area of the tank is 220 cm², what is the water level in the tank?

Solution:
2 ℓ 750 ml = 2 750 cm³

Water level = volume of liquid in a rectangular tank/Base Area of tank

= 2750 cm³/220 cm³

= 12.5 cm (ans)

 

3. Changes to Volume of Water and Water Level

 

 

 

 

 

 

The two tanks above are identical but they contain different volumes of water. When we compare the tanks, we see that the lengths and breadths are the same. This means the base area of both tanks are also the same. Only the water levels are different.

When water is added into or removed from a container, it is important to relate the volume changes to the rise and fall of the water level. We must remember that while the water level changes, the base area of the container will remain the same.

Example

Water is poured into the tank below until it is 1/3 filled. How many 500 ml bottles of water are required to fill the tank to 5/6 of its height?

Solution:

Current water level = 1/3 × 30 = 10
Required water level = 5/6 × 30 = 25
Increase in water level = 25 – 10 =15 cm
Volume of water needed to increase water level by 14 cm = 40 × 20 × 15 = 12000 cm³
No. of 500 ml bottles needed for 12000 cm³ of water = 12000 ÷ 500 = 24 (ans)

Practice 1

Water is poured into a tank measuring 40 cm by 30 cm by 35 cm until it is 4/5 filled. A tap connected to the tank is used to fill some 300 ml bottles to capacity. How many such bottles of water had been filled if the tank is now 3/7  filled?

Solution:

Water level at first = 4/5 × 35 = 28
Water level in the end = 3/7 × 35 = 15
Decrease in water level = 28 – 15 =13 cm
Volume of water used to fill bottles = 40 × 30 × 13 = 15600 cm³
No. of 300 ml bottles filled using 15600 cm³ of water = 15600 ÷ 300 = 52 (ans)

4. Transfer of water from one container to another

Recall that when water is added into or removed from a container, the water level changes but the base area remains the same as there is no change in container.

However when water is transferred from one container to another, the volume of the water remains the same, but the dimensions (length, breadth and/or water level) will change since the new container will have different measurements from the original container. This is shown in the diagram below.

Example

A rectangular tank A measures 24 cm by 16 cm by 8 cm is filled to its brim with water.
When all the water from tank A is poured into a cubical tank B, tank B is 3/4 filled. What is the length of tank B?

Solution:
Volume of water in tank A = 24 cm × 16 cm × 8 cm = 3072 cm³
3/4 of tank B has a volume of 3072 cm³
1/4  of tank B has a volume of 3072 ÷ 3 = 1024 cm³
Capacity of cubical tank B = 1024 × 4 = 4096 cm³
4096 = 16 × 16 ×16

Ans: 16 cm

Practice

A rectangular tank X measuring 25 cm by 8 cm by 10 cm is 4/5 filled with water. When all the water in tank X is transferred to another rectangular tank Y measuring 20 cm by
10 cm by 12 cm, what is the depth of water in tank Y?

Solution:

Water level in tank X = 4/5 ×10 = 8
Volume of water in tank X (to transfer to tank Y) = 25 cm × 8 cm × 8 cm = 1600 cm³
Base area of tank Y = 20 cm × 10 cm = 200 cm²
Water level in tank Y = 1600 cm³ ÷ 200 cm² = 8 cm (ans)

5. Transfer of Water to Equal Water level

In the diagram below, containers A and B contain water up to the same depth.

While the water level in both containers is the same, both containers do not contain the same volume of water because the base areas for the containers are different. Since the base are of container B is much smaller compared to container A, container B would contain less water for the same water level as container A.

Now, if only container A has water, how can we find out how much water to transfer from container A into container B, such that the water levels in both containers are the same?

To do this, we will need to redistribute the amount of water over the total base area of containers A and B. Imagine the following when containers A and B are joined.

When the partitions between containers A and B allow water to pass through, water in container A will flow into container B, until the water level in both containers are the same.

Note that:
Volume of water = Total base area of A and B × Final water level

Example

Container A measuring 24 cm by 10 cm by 18 cm is 2/3 filled with water. Container B with a square base of sides 12 cm is empty. Some water from container A is later
transferred to container B until the water level in both containers are the same. How much water is transferred from container A to container B? Express your answer in
litres and millilitres.

Solution:
Volume of water in container A = 2/3 × 24 × 10 × 18 = 2880 ³
Base area of container A = 24 × 10 = 240 cm²
Base area of container B = 12 cm × 12 cm = 144 cm²
Total base area of A and B = 240 cm² + 144 cm2 = 384 cm²
New water level = 2880 cm³ ÷ 384 cm² = 7.5 cm
Amount of water transferred into container B = 144 cm2 × 7.5 cm
= 1080 cm³
= 1 ℓ 80 ml (ans)

Practice
Container X measuring 12 cm by 8 cm by 10 cm is 4/5 filled with water. Container Y measuring 8 cm by 6 cm by 16 cm is 1/8 filled with water . Some water from container X is later transferred to container Y until the water level in both containers are the same. How much water was transferred into container Y?

Solution:
Volume of water in container X = 4/5 ×12 × 8 × 10 = 768 ³
Volume of water in container Y = 1/8 ×8 × 6 × 16 = 96 ³
Total amount of water to be redistributed into A and B = 768 cm³ + 96 cm³ = 864 cm³
Base area of container A = 12 × 8 = 96 cm²
Base area of container B = 8 cm × 6 cm = 48 cm²
Total base area of A and B = 96 cm² + 48 cm² = 144 cm²
New water level = 864 cm³ ÷ 144 cm² = 6 cm
Decrease in water level of container X = 4/5 × 10 − 6 = 2
Amount of water transferred to container Y = 96 cm² × 2 cm = 192 cm³ (ans)

Practice 2
Tanks P and Q are rectangular tanks. Tank P contains water up to a height of 12 cm while tank Q is empty. When Joe transfers 150 cm³ of water from tank P to tank Q, he
noted that the water level in tank P decreases by 3 cm while the water level in tank Q measures 2 cm.
Ken then transfers more water from tank P to tank Q until the water level in tank Q is twice the water level in tank P.
(a) What is the final water level in tank Q?
(b) How much water did Ken transfer from tank P to tank Q?

Solution:
(a)

A volume of 50 cm³ of water in tank P has a depth of 1 cm.
Base area of tank P = 150 cm³ ÷ 3 cm = 50 cm²
Total volume of water in tank P = 50 cm² × 12 cm = 600 cm³
A volume of 150 cm³ of water in tank Q has a depth of 2 cm.
Base area of tank Q = 150 cm³ ÷ 2 cm = 75 cm²
*Since the final water level in tank Q is two times that of tank P, we must add the base
area of tank Q twice to the total base area.
*Total base area = 50 cm2 + 75 cm² + 75 cm² = 200 cm²
Water level in tank P after redistributing = 600 cm³ ÷ 200 cm² = 3 cm
Water level in tank Q after redistributing = 3 cm × 2 = 6 cm (ans)

(b)
Final volume of water in tank Q = 75 cm² × 6 cm = 450 cm³
Volume of water transferred by Ken = 450 cm³ – 150 cm³ = 300 cm³ (ans)

Conclusion

Understanding how to find the volume of liquid in rectangular containers is an
important skill in everyday life and in exams like the PSLE

This skill will also come in handy when students advance onto the secondary level. This
topic helps students connect volume with real-life situations such as water storage and
transfer.

By mastering the use of formulas, unit conversions, and relationships between water
level and tank size, students become more confident in solving practical problems
involving volume.

Keep practising these methods to strengthen your understanding and accuracy.

Before you go, you might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.

This will be delivered to your email inbox.

Click here to download

Does your child need help in his or her studies?

1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success.  Here are the services we provide:

– Live Zoom lessons

– Adaptably™, an innovative smart learning platform featuring thousands of PSLE and exam-based questions tailored for your child’s practice. Adaptably not only tracks your child’s progress but also identifies their strengths and areas for improvement, providing valuable insights to enhance their learning journey.

– 24/7 Homework Helper Service

We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.

We specialise in English, Math, Science and Chinese subjects.

You can see our fees and schedules here >>

Primary Math Tuition

Secondary Math Tuition

2) Pre-recorded Online courses on Jimmymaths.com

 

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.

Your child can:

– Learn from recorded videos

– Get access to lots of common exam questions to ensure sufficient practice

– Get unlimited support and homework help

You can see the available courses here >>

Math Online Courses