
16 Hardest PSLE Math Questions and How to Approach Them
The Primary School Leaving Examination (PSLE) is known for having challenging questions that often leave students stumped. These maths problems often require unique approaches, and by carefully reading and breaking down the questions, students will be able to solve them.
If your child struggles with these challenging questions, our PSLE math tuition programmes use the proven K-C-A method to help students master even the toughest problem sums.
Here are 16 of the most challenging questions that students encountered in past PSLE Maths papers, and how to solve them!
Before you read on, you might want to enrol in this FREE Math Online Course on 5 Challenging PSLE Math Questions.
You will learn many useful methods to solve tough problem sums!
![]()
Click here to enrol for free >> https://jimmymaths.digitrio.online/product/5-challenging-questions-psle-math-free-online-course/
Fraction of Remainder
At first, John had some money. He spent 1/4 of it on a T-shirt and 2/5 of the remainder on a pair of shoes. After that, his parents gave him $120. The ratio of the total amount of money he had at the end to the amount of the money he had at first was 5 : 4.
How much did John have at first?
Solutions:
Remainder -> 1 – 1/4 = 3/4
Fraction of money left -> 3/5 ×3/4 = 9/20
Since his parents gave him $120, the amount of money left = 9u + 120, while the amount of money at first is 20u.
We can now express them in the given ratio.
9u + 120 : 20u
= 5 : 4
We can now cross-multiply them to find the value of 1 unit.
4 × (9u + 120) = 5 × 20u
36u + 480 = 100u
64u = 480
1u = 7.5
20u = $150 (Ans)
Click the video below to watch the solutions:
2. Before-Change-After
Mrs Hoon made some cookies to sell. 3/4 of them were chocolate cookies and the rest were almond cookies. After selling 210 almond cookies and 5/6 of the chocolate cookies, she had 1/5 of the cookies left. How many cookies did Mrs Hoon sell?
Solutions:
We can use a Before-Change-After table to solve this question.
We need to multiply the Chocolate and Almond cookies by 2 in order the make the chocolate cookies a multiple of 6.
| C | A | Total | |
|---|---|---|---|
| Before | 3 | 1 | 4 |
| 6u | 2u | 8u | |
| Change | − 5u | − 210 | × 1⁄5 |
| After | 1u | 0.6u | 1.6u |
We can now find the difference between the Almond cookies at the start and in the end and equate this to the cookies sold to find the value of 1 unit.
2u – 0.6u = 1.4u
1.4u = 210
1u = 150
5 × 150 + 210 = 960 (Ans)
Click the video below to watch the solutions:
3. Gap and Difference
In a school hall, chairs were arranged in rows such that there were exactly 9 chairs in each row.
For a concert, Mr Ong brought 6 more chairs into the school hall and rearranged all the chairs. There are now exactly 7 chairs in each row and 12 more rows than before.
How many chairs are there in the school hall for the concert?
Solutions:
Let’s draw some models to help us to understand the question better. 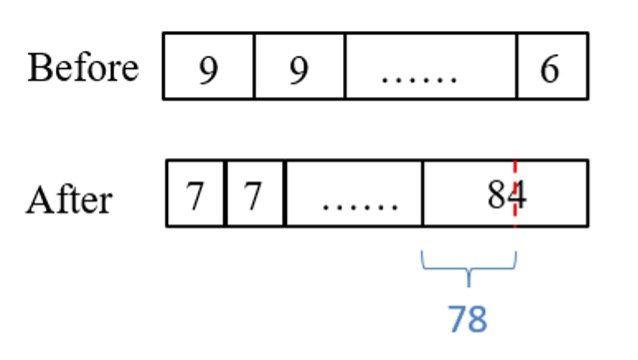
Number of chairs in the extra 12 rows -> 12 × 7 = 84
Since Mr Ong brought 6 more chairs, let’s subtract the 6 chairs away to find the actual difference between all the rows of 9 and rows of 7.
84 – 6 = 78
Difference in each row -> 9 – 7 = 2
Number of rows at first -> 78 ÷ 2 = 39 rows
39 × 9 = 351
351 + 6 = 357 (Ans)
Or
39 × 7 + 84 = 357 (Ans)
Click the video below to watch the solutions:
4. Units and Parts
Jim bought some chocolates and gave half of them to Ken. Ken bought some sweets and gave half of them to Jim.
Jim ate 12 sweets and Ken ate 18 chocolates. After that, the number of sweets and chocolates Jim hade were in the ratio of 1 : 7 and the number of sweets and chocolates Ken had were in the ratio 1 : 4.
How many sweets did Ken buy?
Solutions:
As this question involves 2 unknowns (chocolates and sweets), we can use Units and Parts to solve this question.

Since Jim and Ken gave half of their sweets and chocolates to each other, we can equate their sweets and chocolates to be the same.
1 part = 1 unit + 12 —- (1)
(1) × 4: 4 parts = 4 units + 48
4 parts + 18 = 7 units — (2)
4 parts + 48 + 18 = 7 units
3 units = 66
1 unit = 22
Jim’s sweets at the start = 22 + 12 = 34
Number of sweets Ken bought = 34 × 2 = 68 sweets (Ans)
Click the video below to watch the solutions:
5. Rate of Water Flow
Two rectangular tanks are shown below. 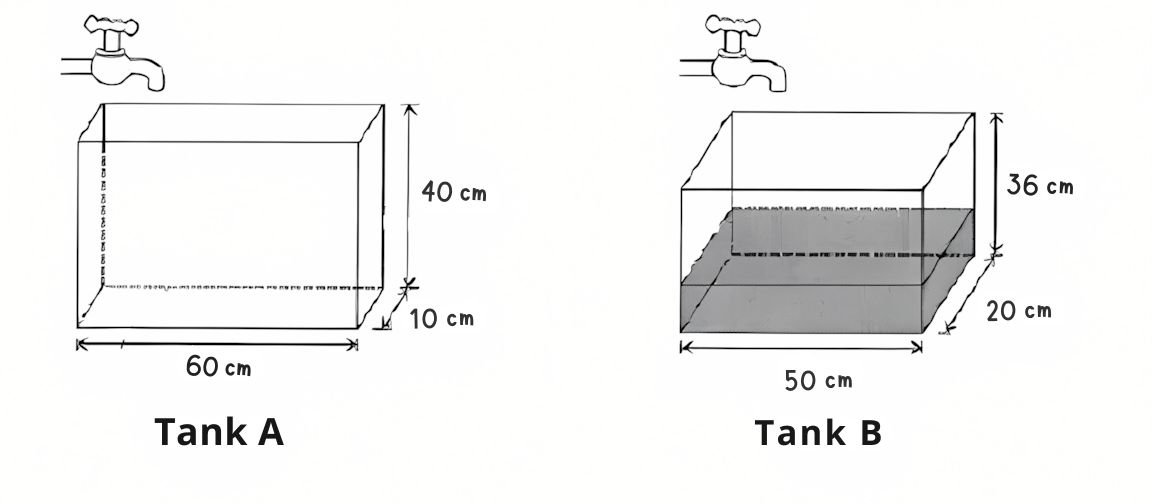 At first, Tank A was empty and one third of Tank B was filled with water. Both taps were turned on at the same time and water from both taps flowed at the same rate of 1.2 litres per minute.
At first, Tank A was empty and one third of Tank B was filled with water. Both taps were turned on at the same time and water from both taps flowed at the same rate of 1.2 litres per minute.
How long did it take for the height of the water to be the same in both tanks?
Solutions:
Base Area of A -> 60 × 10 = 600
Base Area of B -> 50 × 20 = 1000
In 1 min,
Increase in water level of A -> 1200 ÷ 600 = 2
Increase in water level of B -> 1200 ÷ 1000 = 1.2
Difference in rate -> 2 – 1.2 = 0.8
Water level of B at first -> 36 ÷ 3 = 12
Time -> 12 ÷ 0.8 = 15 mins (Ans)
Click the video below to watch the solutions:
6. Assumption
Wei Yang started a savings plan by putting 2 coins in a money box every day. Each coin was either a 20ȼ or 50ȼ coin. His mother also put in a $1 coin in the box every 7 days. The total value of the coins after 182 days was $133.90.
(a) How many coins were there together?
(b) How many of the coins were 50ȼ coins?
Solutions:
(a) Number of $1 coins = 182 ÷ 7 = 26
Total coins put in by Wei Yang = 182 × 2 = 364
364 + 26 = 390 (Ans)
(b) $133.90 – $26 = $107.90
Assume the 364 coins are all 20ȼ
Total: 364 × $0.20 = $72.80
Excess: $107.90 – $72.80 = $35.10
Difference: $0.50 – $0.20 = $0.30
Opposite: $35.10 ÷ $0.30 = 117 (Ans)
Click the video below to watch the solutions:
7. Speed
Mei and Lin took part in a cycling race. Mei cycled at a speed of 20 km/h. Both of them did not change their speed throughout the race. When Lin covered 1/2 of the distance, Mei was 3.5 km in front of her. Mei reached the finishing line at 10.45 a.m. What time did Lin reach the finishing line?
Solutions:
Observe that when Lin covered 1/2 of the distance, Mei was 3.5 km in front of her.
Therefore,
3.5 km × 2 = 7 km (When Lin completed the race, Mei was 7 km in front)
7 km ÷ 20 km/h = 0.35 h (Mei completed the race 0.35 h earlier than Lin)
0.35 h = 21 min
![]()
Click the video below to watch the solutions:
8. Finding Breadth of Rectangle
In the figure below, ABDF and BCEF are rectangles and CDE is a straight line. AB = 6 cm, AF = 8 CM and BF = 10 cm. Find the length of BC.
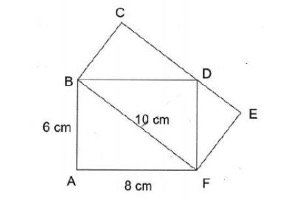
Solutions:
Observe that area of Triangle BDF is half of the area of Rectangle BCEF
Area of 1 triangle = 1/2 × 8 × 6=24
Area of rectangle BCEF = 24 × 2 = 48
48 ÷ 10 = 4.8 (Ans)
Click the video below to watch the solutions:
9. Finding Length of Square
Devi has a square of paper of side 23 cm. She cut along the dotted lines shown in Figure 1 to get one small square of area 49cm² and 8 identical right-angles triangles. Triangle PQR in Figure 2 is one such triangle. Find the length of PQ
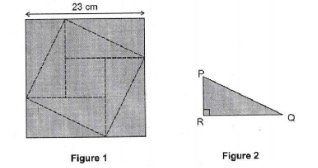
Solutions:
Length of small square in the middle = √49 = 7cm
Length of PR = (23 – 7) ÷ 2 = 8
Length of RQ = 7 + 8 = 15
Area of triangle PRQ = 1/2× 8 × 15 = 60
Area of square ABCD = 60 × 4 + 49 = 289
Length of PQ = √289 = 17 cm (Ans)
Click the video below to watch the solutions:
10. Area and Perimeter
The figure shows a rectangular grass patch and an L-shaped footpath. The width of the footpath is 100 cm. The footpath is tiled using 38 circular tiles of diameter 50 cm, following the pattern shown below. Each tile is in contact with those next to it.
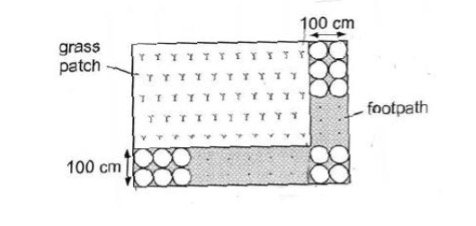
(a) What is the area of the footpath not covered by the tiles? Taken π = 3.14
(b) What is the perimeter of the grass patch?
(a)
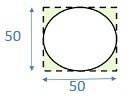
Consider 1 circular tile,
Area not covered -> 50 × 50 – 3.14 × 25 × 25 = 537.5
Total area not covered -> 537.5 × 38 = 20 425 cm² (Ans)
(b)
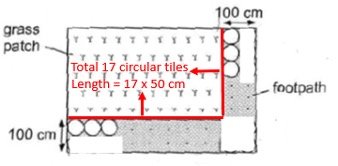
Observe that there are 4 circular tiles in the bottom right hand corner.
38 – 4 = 34
Next, observe that there are 2 rows of circular tiles in the footpath.
34 ÷ 2 = 17 (There are 17 circular tiles in 1 length and 1 breadth of the grass patch)
Lastly, observe that the grass patch is made up of 2 lengths and 2 breadths.
2 × 17 × 50 cm = 1700 cm (Ans)
Click the video below to watch the solutions:
11. Cubes and Cuboids
Ravi had a rectangular block of wood 10 cm by 5 cm by 4 cm.
He painted all the faces of the block.
(a) What is the total painted area?
(b) Ravi cut the block into 1-cm cubes. How many of these cubes have
(i) none of the faces painted?
(ii) 2 of the faces painted?

Solutions:
(a) Top surface area + Bottom surface area = 2 × 10 cm × 5 cm = 100 cm²
Left surface area + Right surface area = 2 × 5 cm × 4 cm = 40 cm²
Front surface area + Back surface area = 2 × 10 cm × 4 cm = 80 cm²
Total painted surface area = 100 cm² + 40 cm² + 80 cm² = 220 cm² (Ans)
(b)(i)
Remaining Breadth = 5 – 2 = 3
Remaining Length = 10 – 2 = 8
Remaining Height = 4 – 2 = 2
Number of cubes without painted surface = 8 × 3 × 2 = 48 (Ans)
(b)(ii)
Number of cubes with 2 painted surfaces along the length
= 4 sets of (10 – 2)
= 4 × 8 = 32
Number of cubes with 2 painted surfaces along the breadth
= 4 sets of (5 – 2)
= 4 × 3 = 12
Number of cubes with 2 painted surfaces along the height
= 4 sets of (4 – 2)
= 4 × 2 = 8
Total number of cubes with 2 painted surfaces
= 32 + 12 + 8
= 52 (Ans)
Click the video below to watch the solutions:
![]()
12. Fractions
Pupils in a school are put into two groups for a learning journey. 2/5 of the pupils are in Group A and the rest are in Group B. 1/4 of the pupils in Group A are girls. In the school, 3/10 of the pupils are girls. What fraction of the pupils in Group B are girls?
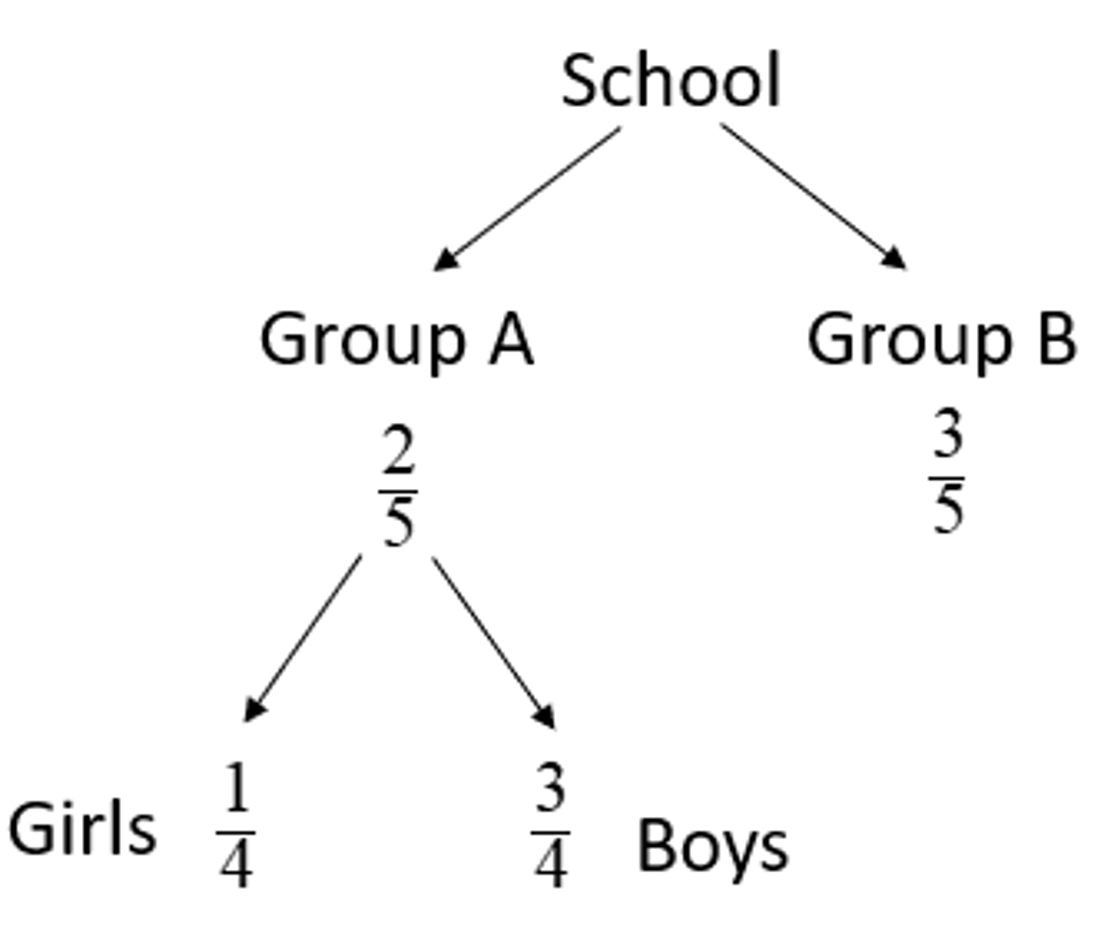
Girls in A -> 1/4×2/5 = 1/10
Girls in B -> 3/10-1/10 = 2/10
Girls in B -> 3/10-1/10 = 2/10 = 1/5
Fraction of girls in B × 3/5 = 1/5
Fraction of girls in B = 1/5 ÷3/5
= 1/5 × 5/3
= 1/3 (Ans)
Click the video below to watch the solutions:
![]()
13. Volume
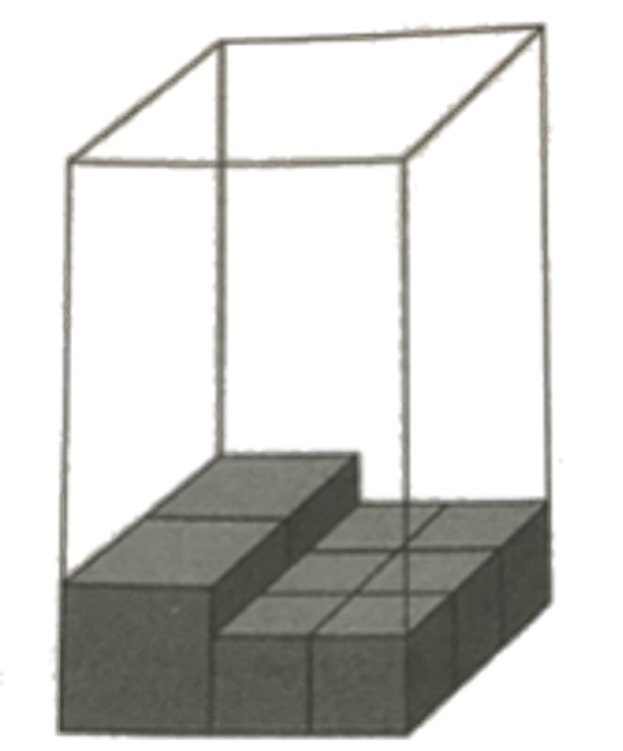
Jack has 8 identical large cubes and some identical small cubes. He packed all the cubes tightly into a rectangular box such that cubes of the same size are stacked on top of each other. The box is filled to its brim exactly. The figure shows the first layer of cubes packed in the box.
a) How many small cubes does Jack have?
b) The volume of the box is 4032 cm³. The total volume of the 8 large cubes is 3/7 of the volume of the box. What is the length of one edge of the small cube?
Solutions:
(a)
1 L = 1.5 S
4 L = 6 S
6 × 6 = 36 (Ans)
(b)
Volume of 8 L cubes -> 3/7×4032= 1728 cm³
Volume of 36 S cubes ->4032 – 1728 = 2304 cm³
Volume of 1 S cubes ->2304 ÷ 36 = 64 cm³
![]()
Click the video below to watch the solutions:
14. Percentage Discount
Jamie and Oliver used $61.20 each to buy some egg tarts. Jamie has a 15% discount coupon and bought 6 more egg tarts than Oliver.
(a) How many egg tarts did Jamie buy?
(b) What is the cost of an egg tart without the discount?

Solutions:
(a)
15% -> 6 egg tarts
1% -> 0.4
100% -> 40 (Ans)
b)
Oliver’s egg tarts ->40 – 6 = 34
Original price -> $61.20 ÷ 34 = $1.80 (Ans)
Or,
Discounted Price -> $61.20 ÷ 40 = $1.53
Original price -> $1.53 ÷ 85 × 100 = $1.80 (Ans)
Click the video below to watch the solutions:
![]()
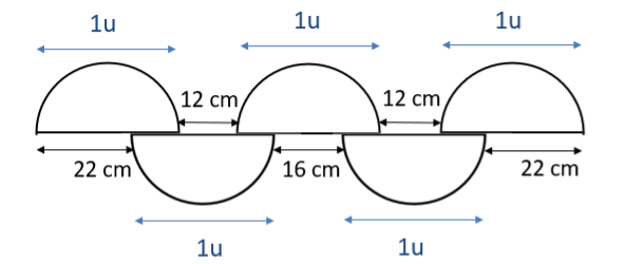
15. Circles
Five identical semi-circles are arranged as shown. Find the diameter of one circle. 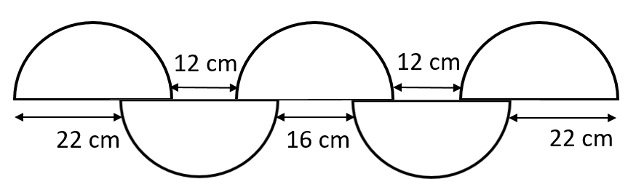
Solutions:
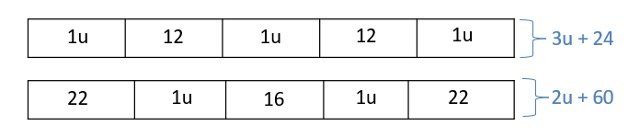
Since they are the same length, we can equate them.
3u + 24 = 2u + 60
3u – 2u = 60 – 24
1u = 36 cm (Ans)
Click the video below to watch the solutions:
![]()
16. Patterns
Study the pattern below and answer the questions. 
| Figure | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| White triangles | 1 | 1 | 6 | 6 | |
| Grey triangles | 0 | 3 | 3 | 10 | |
| Total | 1 | 4 | 9 | 16 | 25 |
(a) Fill in the table above.
(b) Find the total number of white and grey triangles for Fig. 250.
(c) Find the percentage of grey triangles in Fig. 250.
Solutions:
(a)

(b) Fig. number × Fig. number 250 × 250 = 62500 (Ans)
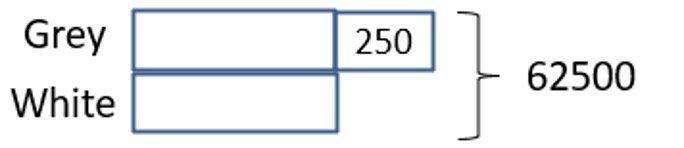
(c)
62500 – 250) ÷ 2 = 31125
Grey -> 31125 + 250 = 31375
Percentage of grey triangles = 31375/62500 × 100% = 50.2% (Ans)
Click the video below to watch the solutions:
![]()
Before you read on, you might want to enrol in this FREE Math Online Course on 5 Challenging PSLE Math Questions.
You will learn many useful methods to solve tough problem sums!
![]()
Click here to enrol for free >> https://jimmymaths.digitrio.online/product/5-challenging-questions-psle-math-free-online-course/
Does your child need help in his or her studies?
1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:
- Live Zoom lessons
- Adaptably™, an innovative smart learning platform featuring thousands of PSLE and exam-based questions tailored for your child’s practice. Adaptably not only tracks your child’s progress but also identifies their strengths and areas for improvement, providing valuable insights to enhance their learning journey.
- 24/7 Homework Helper Service
We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities. We specialise in English, Math, Science and Chinese subjects. You can see our fees and schedules here >> https://gradesolution.com.sg/schedule/
2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses. Your child can:
- Learn from recorded videos
- Get access to lots of common exam questions to ensure sufficient practice
- Get unlimited support and homework help
You can see the available courses here >> https://jimmymaths.digitrio.online/our-courses/
