Ever looked at a math problem that combines algebra and fractions and felt a pang of dread?
It’s completely normal to feel this way. The mix of variables and fractions can look intimidating and complex.
Take this equation, for example \(\frac{x}{2} + \frac{3}{x + 1} = \frac{3x – 5}{4x + 4}\). Should we simplify, make one side become zero, or multiply everything?
Most students I work with struggle with these kinds of problems, even the strong ones. But don’t worry—here’s a game-changer: Cross multiplication is like a shortcut on a long journey. It simplifies solving algebraic fractions by providing a direct path.
In this article, I’ll show you how all you need to know about cross multiplication and how it can make these problems easier. This technique, called cross multiplication, is crucial for understanding algebraic methods for solving equations. Think of it as your GPS for navigating tricky math problems. Let’s dive in!
Before you read on, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.

What is Cross Multiplication?
Cross multiplication is a mathematical technique used to solve equations involving fractions. It is a method of multiplying two fractions to eliminate the denominators and solve for the unknown variable. This technique is particularly useful in algebra, where it simplifies the process of dealing with equations that include fractions. By cross multiplying, we can transform a complex fraction equation into a more manageable linear equation, making it an essential skill for students to master.
How is Using Cross Multiplication a Shortcut?
Example: Solve \(\frac{3}{x} = \frac{4}{5}\)

From the example above, can you see how cross multiplication acts as a powerful shortcut to eliminate fractions from equations?
Instead of multiplying each denominator separately on both sides, cross multiplication allows us to handle both denominators simultaneously.
By doing so, we effectively “cross out” the fractions, transforming a complex equation with algebraic fractions into a simpler linear equation in just one step.
It’s like killing two birds with one stone, saving time and reducing the potential for mistakes.
This technique streamlines the process, making it much easier to focus on solving for the variable without getting bogged down in fraction manipulation.
It’s short and sweet, neat and clean. However, you can’t always use cross multiplication to solve algebraic equations. It’s a powerful tool, but only if you apply it correctly.
So, when can you actually use this technique? Let’s explore the different scenarios.
2. When to Use Cross-Multiplication Correctly?
To apply cross multiplication effectively, it’s important to identify the right context. Here are some key traits to help you determine when to use this technique:
a. Fraction = Fraction:
Cross multiplication is primarily used when two fractions are set equal to each other. This method helps simplify the equation by eliminating the fractions. If there’s no equal sign, the problem might require simplification or another method.
Example:

b. Fraction with an Inequality Sign:
Cross multiplication can also be applied to inequalities involving fractions, such as \(\frac{a}{b} < \frac{c}{d}\) or \(\frac{a}{b} \geq \frac{c}{d}\). When using cross multiplication for inequalities, remember to reverse the inequality sign if you multiply or divide by a negative number.

c. Single Fraction on Each Side:
Each side of the equation or inequality must have only one fraction. If there are multiple fractions on one or both sides, simplify them into single fractions first before using cross multiplication.
Example:
\[\frac{x + 1}{2} = \frac{3}{4}\]
If an equation appears like \(\frac{x + 1}{2} + \frac{1}{3} = \frac{3}{4}\), first combine \(\frac{x + 1}{2} + \frac{1}{3}\) into a single fraction before applying cross multiplication.
d. Look out for the command word ‘Solve’:
The problem should explicitly instruct you to solve the equation or inequality. If the question asks for simplification or evaluation, cross multiplication may not be suitable.
Example:

e. Making the subject of a formula:
Cross-multiplication can also be useful when you need to make a variable the subject of a formula, especially if the formula involves algebraic fractions.
Example:
Given the formula \(\frac{5}{x – 1} = \frac{7}{y}\), you can use cross-multiplication to isolate \(x\).
For more details on how to make the subject of a formula, view the revision note “How to Make the Subject of the Formula” >> (https://jimmymaths.digitrio.online/how-to-make-the-subject-of-the-formula/)
In a nutshell, it’s essential to ensure that the conditions are right: the fractions must be set equal (or as an inequality) to each other, there should be only one fraction on each side of the equation, and the problem should involve solving rather than simplifying. Additionally, cross-multiplication can be effectively used when making a variable the subject of a formula, especially if the formula involves algebraic fractions.
Use the decision tree below to guide you through the process of identifying the correct scenarios for applying this technique, ensuring you avoid common pitfalls and solve equations with precision.
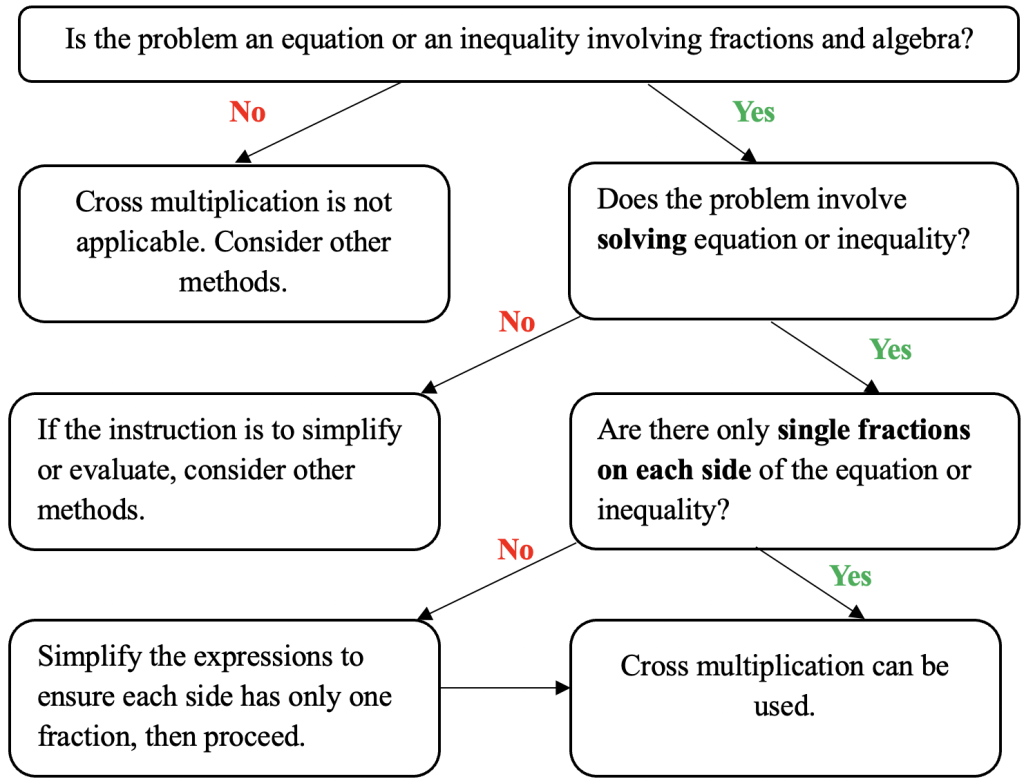
3. Mastering Cross Multiplication: Applying the Technique to Challenging Questions
Now that we’ve covered the fundamentals of cross multiplication and when to use it correctly, let’s dive into mastering this technique by applying it to more complex questions.
This will not only strengthen your understanding but also prepare you for more challenging problems, such as those you might encounter in exams.
Example
Solve the equation below.
\[\frac{x + 2}{x^{2} – 4} – \frac{3}{x – 2} = 3\]
Solutions:
\[\frac{x + 2}{x^{2} – 4} – \frac{3}{x – 2} = 3\]
Applying special identity, \(a^{2} – b^{2} = (a – b)(a + b)\),
\[\frac{x + 2}{(x – 2)(x + 2)} – \frac{3}{x – 2} = 3\]
Find the LCM of the denominator to combine them into a single algebraic fraction.
LCM = (x-2)(x+2)
\[\frac{x + 2}{(x – 2)(x + 2)} – \frac{3(x + 2)}{(x – 2)(x + 2)} = 3\]
\[\frac{x + 2}{(x – 2)(x + 2)} – \frac{3x + 6}{(x – 2)(x + 2)} = 3\]
Combine, Simplify & Factorize,
\[\frac{x + 2 – (3x + 6)}{(x – 2)(x + 2)} = 3\]
\[\frac{x + 2 – 3x – 6}{(x – 2)(x + 2)} = 3\]
\[\frac{- 2x – 4}{(x – 2)(x + 2)} = 3\]
\[\frac{- 2(x + 2)}{(x – 2)(x + 2)} = 3\]
Cross Multiply the Fractional Equation,
\[\frac{- 2}{x – 2} = \frac{3}{1}\]
\[- 2 = 3(x – 2)\]
Add 6 on both sides,
\[- 2 + 6 = 3x – 6 + 6\]
\[4 = 3x\]
Divide 3 on both sides,
\[\frac{4}{3} = \frac{3x}{3}\]
\[\frac{4}{3} = x \text{ (Ans)}\]
Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.

Does your child need help in his or her studies?
Find out more about our Math Tuition Class Free Trial.
1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:
– Live Zoom lessons
– Adaptably, a smart learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital questions.
– 24/7 Homework Helper Service
We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities. We also offer a free trial class and consultation with our tutors, to help make sure we are the best fit for your child.
We specialise in English, Math, Science, and Chinese subjects.
You can see our fees and schedules here >>
2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.
Your child can:
– Learn from recorded videos
– Get access to lots of common exam questions to ensure sufficient practice
– Get unlimited support and homework help
You can see the available courses here >>
