ASTC Trigo Rule – How to Solve Trigo Equations
In this revision note, you will learn about the ASTC Trigo rule and how to use it to solve Trigonometry (Trigo) equations in O-Levels A-Math exams.
Before you read on, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.
Cartesian Plane
The cartesian plane can be divided into 4 equal parts. Each part is called a quadrant. We name each of the quadrant as shown in Figure 4 below.
Basic Angle or Reference Angle
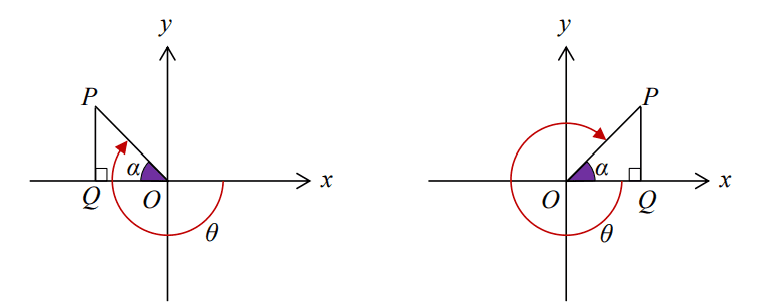
Corresponding to each angle formed by the rotation of OP about the origin O, a unique acute angle (also commonly called the basic angle or reference angle or α) and a right-angled triangle OPQ can be observed, where Q is always on the x-axis such that ∡ is 90°. The figure below shows the relationship between the positive angle θ and basic angle α for each quadrant.
θ in 2nd Quadrant θ in 1st Quadrant
θ = 180° – α θ = α
θ in 3rd Quadrant θ in 4th Quadrant
θ = –( 180° + α) θ = – (360° – α)
Negative Angle
The figure below shows the relationship between the negative angle θ and basic angle α for each quadrant
θ in 2nd Quadrant θ in 1st Quadrant
θ = –( 180° + α) θ = –( 360° – α)
θ in 3rd Quadrant θ in 4th Quadrant
θ = –( 180° – α) θ = – α
ASTC Trigo Rule
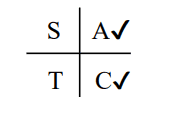
To remember which trigonometric ratios are positive, your can follow the ASTC Trigo rule: ASTC (Add Sugar To Coffee).
The figure below explains the ASTC Trigo rule and why the trigonometric ratios are positive in each quadrant.
|
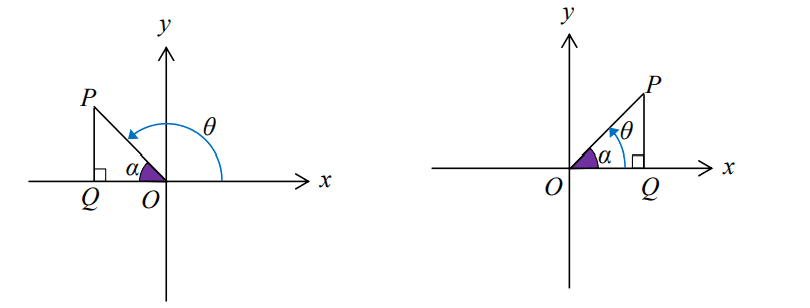
θ in 2nd Quadrant θ = 180° – α sin θ = sin α = PQ/OP cos θ = cos α = –OQ*/OP tan θ = tan α = –PQ/OQ* *OQ is negative in the value since it is on the negative side of the x-axis. Only sine ratio in this quadrant is positive
|
θ in 1st Quadrant θ = α sin θ = sin α = PQ/OP cos θ = cos α = –OQ/OP tan θ = tan α = –PQ/OQ OQ and PQ are on the positive sides of the axes The hypotenuse is always positive in each quadrant. All trigonometric ratios in this quadrant are positive. |
|
θ in 3rd Quadrant θ = 180° + α sin θ = sin α = – PQ* /OP cos θ = cos α = –OQ*/OP tan θ = tan α = PQ*/OQ* *OQ is negative in the value since it is on the negative *PQ is negative in value since it is on the negative side of the y-axis. side of the x-axis. Only tangent ratio in this quadrant is positive since both PQ and OQ are negative. |
θ in 4th Quadrant θ = 360° – α sin θ = sin α = –PQ*/OP cos θ = cos α = OQ/OP tan θ = tan α = –PQ*/OQ * PQ is negative in value since it is on the negative side of the y-axis. Only cosine ratio in this quadrant is positive.
|
Example of Solving Trigo Equations
Solve the following equations for 0° ≤ x ≤ 360°.
(a) cos x = 0.1256 (b) sin x = −1/2 (c) 2 tan x + 3 = 0
Solution:
(a)
cos x = 0.1256
Basic ∡ = 82.7846°
x = 82.7846°, 360° − 82.7846°
= 82.8°, 277.2° (1 dp) (ans)
Since cos x has a positive value, we infer x must be in the 1st or 4th Quadrant.
We will calculate the value of x for each of those quadrants.
In the first quadrant, x is simply the value of the basic angle α.
(b)
sin x = −1/2
Basic ∡ = 30°
x = 180° + 30°, 360° − 30°
= 210°, 330° (ans)
Since sin x has a negative value, we infer x must be in the 3rd or 4th Quadrant.
We will calculate the value of x for each of those quadrants.
Note that the calculation of α involves sin−1(1/2). Leave out the minus sign in the calculator since α is always acute.
(c)
2 tan x + 3 = 0
tan x = −3/2
Basic ∡ = 56.3100°
x = 180° − 56.3100°, 360 − 56.3100°
= 123.7°, 303.7° (1 dp) (ans)
Since tan x has a negative value, we infer x must be in the 2nd or 4th Quadrant.
We will calculate the value of x for each of those quadrants.
Note that the calculation of α involves tan−1(3/2). Leave out the minus sign in the calculator since α is always acute.
Last Minute Revision for O Level Math?
Check out our exam guide on other topics here!
Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.
Does your child need help with Mathematics? Find out more about our Math Tuition Class Free Trial.
1) Live Zoom Lessons at Grade Solution Learning Centre
At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:
– Live Zoom lessons
– EdaptIQ™, a smart learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital worksheets.
– 24/7 Homework Helper Service
We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities. We also offer a free trial class and consultation with our tutors, to help make sure we are the best fit for your child.
We specialise in English, Math, and Science subjects.
You can see our fees and schedules here >>
2) Pre-recorded Online courses on Jimmymaths.com
If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.
Your child can:
– Learn from recorded videos
– Get access to lots of common exam questions to ensure sufficient practice
– Get unlimited support and homework help
You can see the available courses here >>