Does your child get confused when calculating the area of a trapezium? You’re not alone! Many Primary School students find trapeziums tricky because this four-sided shape looks similar to other quadrilaterals—but the formula is quite different.
A trapezium (also called a trapezoid in some countries) is a special polygon with one pair of parallel sides called bases. The other two sides are not parallel to each other, which gives the trapezium its unique slanted appearance. To find its area, you need to know the lengths of both bases and the perpendicular height—the shortest distance between the parallel lines.
The good news? Once you understand the area of trapezium formula, it becomes much easier to solve.
In this guide, we’ll break down each part of the trapezium step by step:
- What a trapezium is and how to identify one
- How the area of trapezium formula works and why
- Step-by-step worked examples your child can follow
- Real-world applications to make learning meaningful
Whether your child is in Primary 5, Primary 6, or preparing for PSLE, this guide will help them build confidence in solving trapezium problems.
Before you read on, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.

What is a Trapezium?
A trapezium is a special four-sided shape in geometry. Here are some important things to know:
- It has one pair of opposite sides that are parallel. These sides are called bases.
- The other two sides, which are not parallel, can be of different lengths and slant in various ways.
- Trapeziums come in many shapes, but they always have one pair of parallel
The following are some examples of trapeziums in 2−D.

Trapeziums are found everywhere, from architecture, rooftops, tables and even in garden designs!

Discovery of Trapeziums in Ancient Architecture
Machu Picchu, the renowned Incan citadel located high in the Andes Mountains of Peru, showcases remarkable architectural ingenuity, with geometric shapes playing a crucial role in its design. It was estimated to have been built in the year 1450
Among these, trapeziums are a prominent feature in its construction. The Inca (indigenous people living in the mountains of Peru) used trapezoidal shapes in doorways, windows, and niches, which were not only aesthetically pleasing but also structurally resilient. This design helped the structures withstand earthquakes by distributing stress more evenly, preventing cracks and collapses.

The trapezoidal form symbolises strength and stability, aligning with the Inca’s deep connection to nature and their ability to harmonise functionality with beauty. This innovative use of geometry highlights their advanced engineering skills and their profound understanding of structural principles.
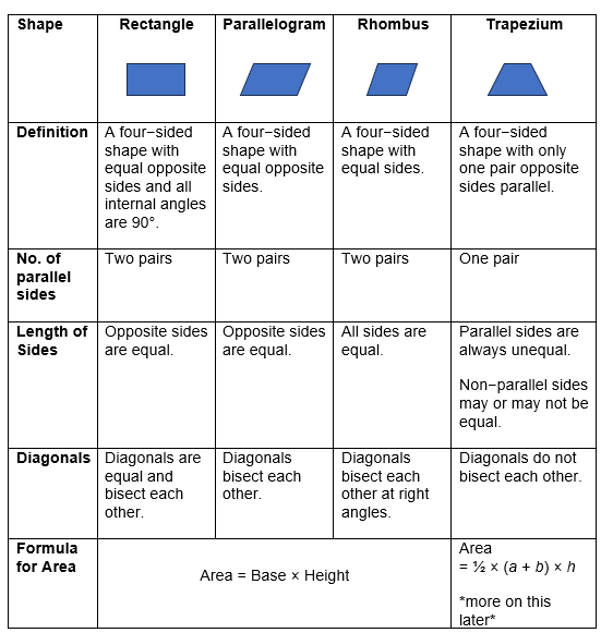
Key Differences Between Common Quadrilaterals
The trapezium can sometimes resemble other quadrilateral shapes that you might have learnt about. The following summarises the key differences between some common quadrilateral shapes.
Parts of a Trapezium
To understand a trapezium better, let us look at its key parts:
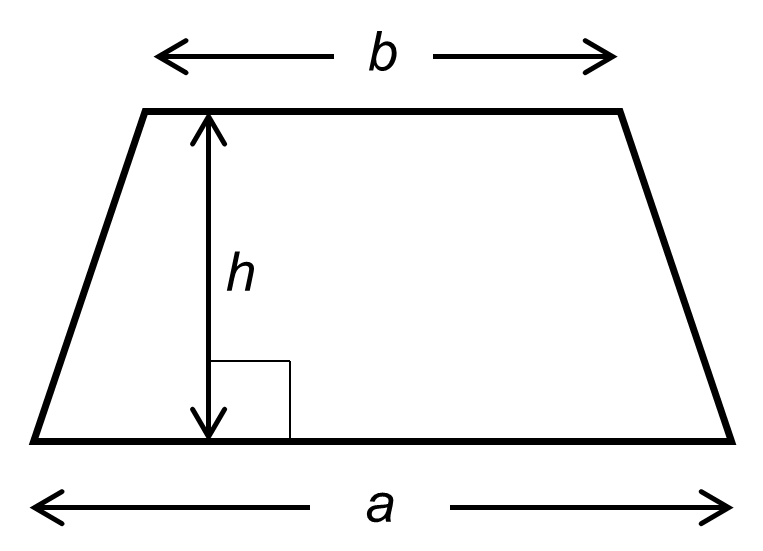
- Bases: These are the two parallel sides of the trapezium. The longer one is usually called “a“, and the shorter one is called “b“.
- Height (h): This is the shortest perpendicular distance between the two bases. It is an essential measurement for calculating the area.
- Non-parallel sides: These are the sides that are not parallel. They give the trapezium its unique shape but are not used in the area calculation.
How is the Formula for Area of a Trapezium Derived?
Note that while the trapezium and parallelogram may at times look similar, the formulae to calculate their respective areas are not the same. Let us review how the formula for the area of a parallelogram is derived pictorially. The diagram below shows a parallelogram, with b as its base and h as its vertical height.
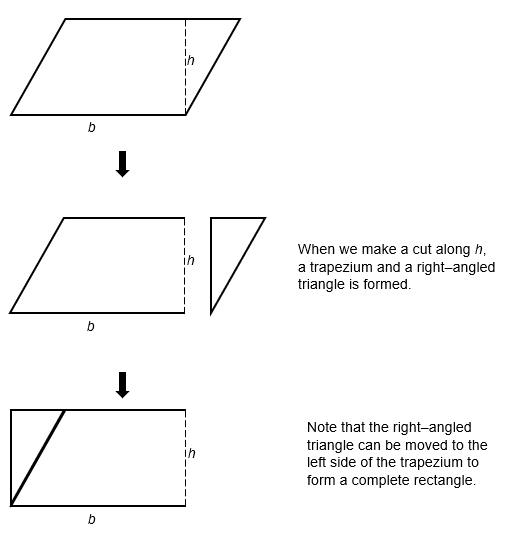
Since the area of the original parallelogram and the newly formed rectangle is the same, we can infer that the formula to calculate the area of the parallelogram and the formula to calculate the area of the rectangle are the same.
So the area of the parallelogram = base (b) × height (h)
On the other hand, a trapezium can be thought of as a combination of two triangles. This is because when a diagonal is drawn inside a trapezium, we have the following two triangles.

See that the area of the trapezium is equal to the sum of area of the two triangles within.
Area of the trapezium = ½ × a × h + ½ × b × h (We can factorise ½ and h)
= ½ × h × (a + b)
Example 1:
The diagram below shows a trapezium, PQRS. The shortest distance between the parallel sides is 6 cm.
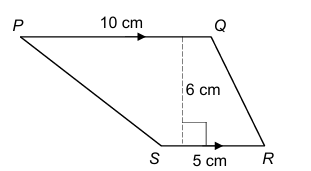
Calculate the area of PQRS.
Solution:
Area of PQRS = ½ × (10 + 5 ) × 6
= 45 cm2 (Ans)
Example 2
The top face of a garden bed shown below is in the shape of a trapezium. The parallel sides of the trapezium are of lengths 2 m and 1.8 m. The garden bed has a depth of 0.5 m.
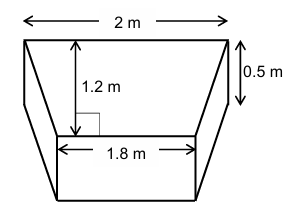
Find the total volume of the garden bed in square metres.
Solution:
Area of trapezium = ½ × (2 + 1.8 ) × 1.2
= 2.28 m2
Volume of flower bed = 2.28 × 0.5
= 1.14 m3 (Ans)
Try It Yourself!
Here are some problems for you to solve:
1. A trapezium has bases of 14 cm and 10 cm, and a height of 6 cm. What is its area? (Ans: 72 cm²)
2. Another trapezium has a longer base of 18 m, a shorter base of 12 m, and a height of 7 m. Calculate its area. (Ans: 105 m²)
Why Is This Important?
Trapeziums are among the many geometric shapes that are part of the GCE Mathematics syllabus. In addition, knowing how to find the area of a trapezium is useful in many real-life situations:
- You can calculate the size of gardens, rooftops, or irregularly shaped rooms.
- Builders and designers use this knowledge to estimate materials for
- Landscapers often work with trapezium shapes when planning spaces.
Understanding trapeziums helps you solve practical problems and makes geometry more meaningful in everyday life.
Conclusion: You’re a Trapezium Expert!
Well done! You now know what a trapezium is, how to identify its parts, and how to calculate its area. Keep practising with different examples, and soon, you will be a master at solving trapezium-related problems. Geometry is not just about shapes—it is about solving real-world challenges. Keep learning and enjoy the journey into the fascinating world of maths!
To find out more about what we can offer, check our Jimmy Maths’ PSLE Math Tuition for Primary School students, or refer to our Revision Notes.
Need More Revision Notes for Primary School Math?
Check out our exam guide on other topics here!
Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.

Does your child need help with Mathematics?
1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:
– Live Zoom lessons
– Adaptably, an AI-Powered learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital questions.
– 24/7 Homework Helper Service
We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.
We specialise in English, Math, Science, and Chinese subjects.
You can see our fees and schedules here >>
2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.
Your child can:
– Learn from recorded videos
– Get access to lots of common exam questions to ensure sufficient practice
– Get unlimited support and homework help
You can see the available courses here >>
