Angle Properties – O Level Exam Preparation Guide
In this revision note, you will learn the all the angle properties and applying them to solve Geometry questions on Polygons.
Different types of angles
a) An acute angle is less than 90°.
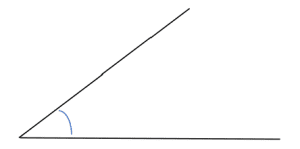
b) A right angle is equal to 90°.
c) An obtuse angle is between 90° and 180°.
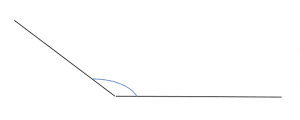
d) A straight line is equal to 180°.
e) A reflex angle is larger than 180° but less than 360°.
f) A complete turn is 360°
Before you read on, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.
Angle Properties
1) Two angles are said to be complementary angles if their sum is 90°.
2) Two angles are called supplementary angles if their sum is 180°.
3) Vertically opposite angles are those on the opposite sides of two intersecting lines.
4) Two angles are said to be corresponding angles if they have the same relative positive at the each intersection where a line cuts across a pair of parallel lines.
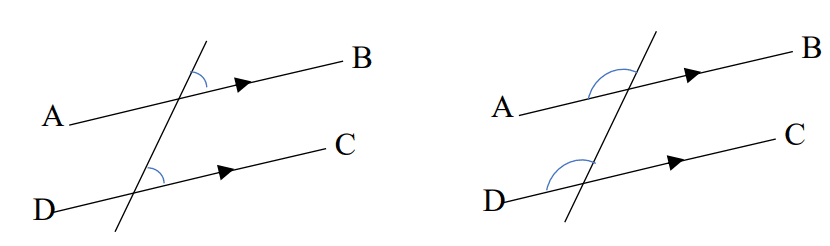
The corresponding angles are equal to each other.
5) Two angles are called alternate angles if they lie on the different side of the line cutting across a pair of parallel lines.
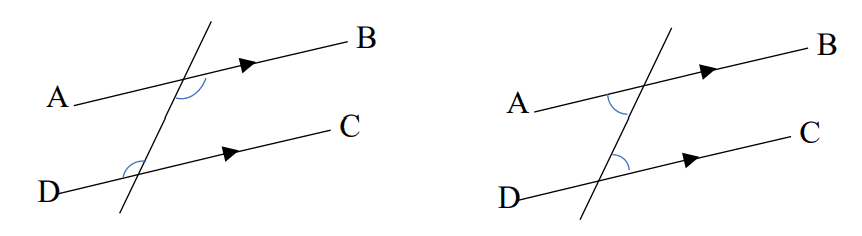
The alternate angles are equal to each other.
6) Two angles are known as interior angles if they lie on the same side of the line that lie on the different side of the line cutting across a pair of parallel lines.
Interior angles add up to 180°.
Angle Properties of Polygons
A polygon is a closed plane figure with three or more straight lines. Polygons are named according to the number of sides they have.
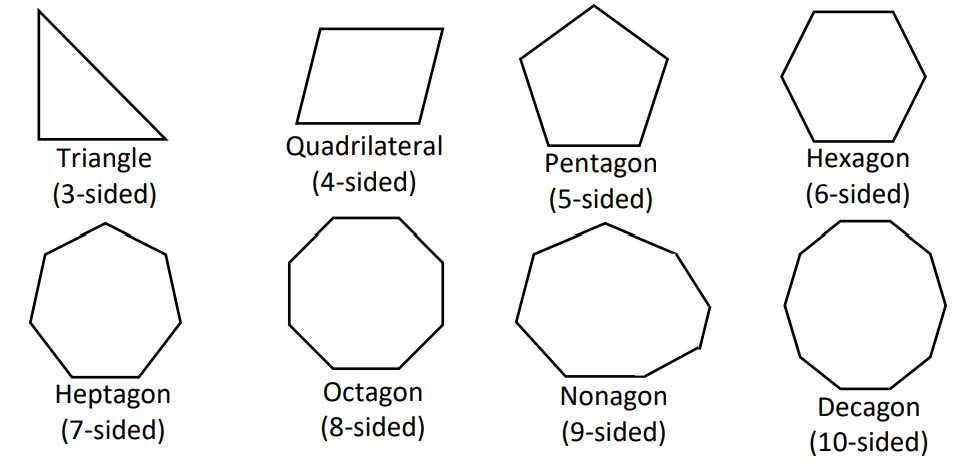
Note: Polygon with n sides is called an n-gon.
A regular polygon is a polygon with all its sides and angles equal.
Angle Properties of Triangles
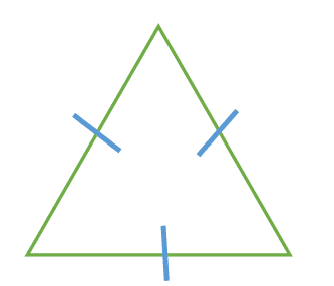
a) An equilateral triangle is a triangle with 3 equal sides. Each of its angles is 60°.
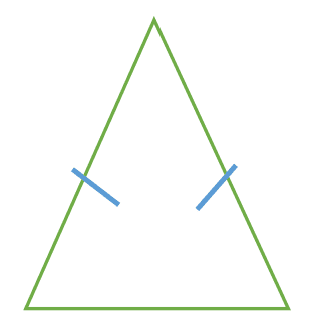
b) An isosceles triangle is a triangle with 2 equal sides. Its base angles are equal.
The sum of the interior angles of a triangle is always 180°.
Angle Properties of Rhombus
- Opposite angles are equal ( ∠a = ∠a )
- ∠a + ∠b = 180° (Interior angles)
- The diagonals bisect the angles equally
- The diagonals intersect at Right Angles
Angle Properties of Parallelogram
- Opposite angles are equal (∠a = ∠a )
- ∠a + ∠b = 180° (Interior angles)
- diagonals DO NOT bisect the angles equally
- diagonals DO NOT intersect at Right Angles
Angle Properties of Trapezium
- ∠a + ∠d = 180° (interior angles formed between parallel lines)
- ∠b + ∠c = 180° (interior angles formed between parallel lines)
- ∠a + ∠d = ∠b + ∠c
Sum of Angles in a Quadrilateral
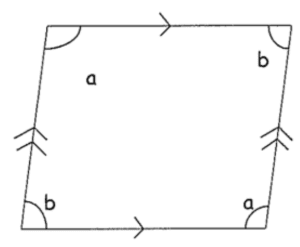
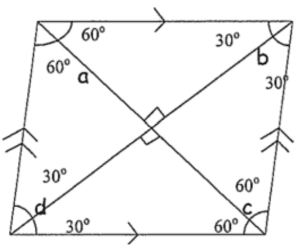
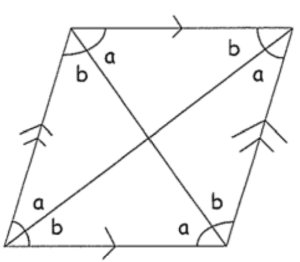
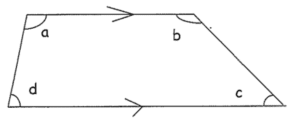
A quadrilateral is a 4-sided polygon. Any quadrilateral can be divided into 2 triangles along its diagonal. Since the angles of a triangle add up to 180°, the angle sum of a quadrilateral is 180° × 2 = 360°.
Sum of Interior Angles in a Polygon
A polygon with n sides has n interior angles.
The sum of interior angles = (n – 2) × 180°.
Sum of Exterior Angles in a Polygon
A polygon with n sides has n exterior angles.
Each pair of interior angle and exterior angle is supplementary (add up to 180°).
The sum of the exterior angles of an n-sided polygon is always 360°
Angle Properties of Polygons Example 1
Find the exterior angle of a 12-sided regular polygon.
Let x the size of each exterior angle.
12 × x = 360°
x° = 30°
Angle Properties of Polygons Example 2
The ratio of an interior angle to an exterior angle of a regular n-sided polygon is 8 ∶ 1. How many sides does the polygon have?
Let 8a and a be the interior angle and the exterior angle at the same vertex respectively.
exterior angle + interior angle = 180° (adjacent ∠s on a straight line)
a + 8a = 180°
a = 20°
Sum of exterior angles = 360°
20°(n) = 360°
n = 18
∴ The polygon has 18 sides.
Last Minute Revision for O Level Math?
Check out our exam guide on other topics here!
Before you go, you might want to download this entire revision notes in PDF format to print it out, or to read it later.
This will be delivered to your email inbox.
Does your child need help with Mathematics? Find out more about our Math Tuition Class Free Trial.
1) Live Zoom Lessons at Grade Solution Learning Centre
At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:
– Live Zoom lessons
– EdaptIQ™, a smart learning platform that tracks your child’s progress, strengths and weaknesses through personalised digital worksheets.
– 24/7 Homework Helper Service
We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities. We also offer a free trial class and consultation with our tutors, to help make sure we are the best fit for your child.
We specialise in English, Math, and Science subjects.
You can see our fees and schedules here >>
2) Pre-recorded Online courses on Jimmymaths.com
If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.
Your child can:
– Learn from recorded videos
– Get access to lots of common exam questions to ensure sufficient practice
– Get unlimited support and homework help
You can see the available courses here >>