5 Tricky MCQs on Fractions

MCQs on Fractions can be challenging for students, especially if they do not know which concepts to apply during an exam.

In this tutorial, we show you how to help your child find solutions to varying tricky MCQs on fractions.

Before you read on, you might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.

This will be delivered to your email inbox.

psle math revision notes

Example 1

This question was taken from the MGS 2022 P6 Prelim.

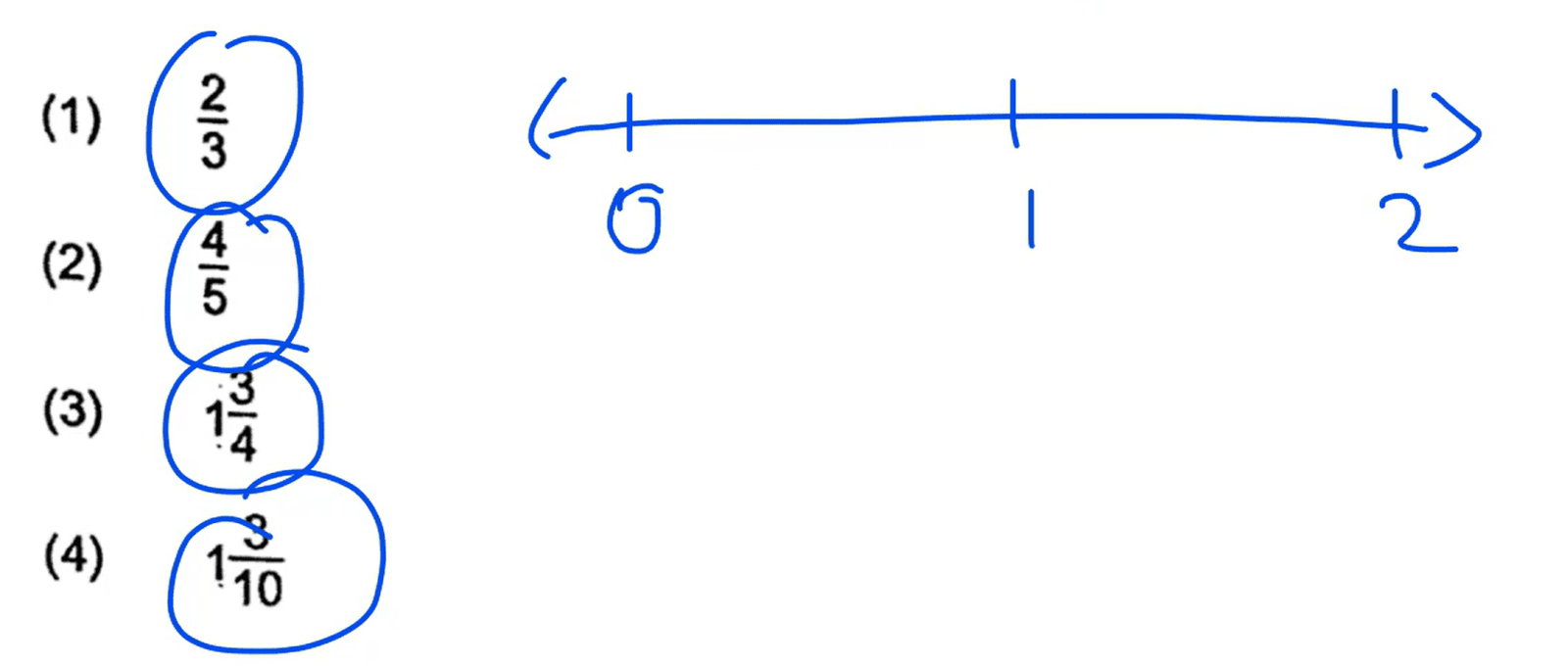
Question: Which of the following fractions is nearest to 1?

tricky mcq

Step 1: Draw a number line.

We can first draw a number line and write “1” in the middle.

$comparing fraction$

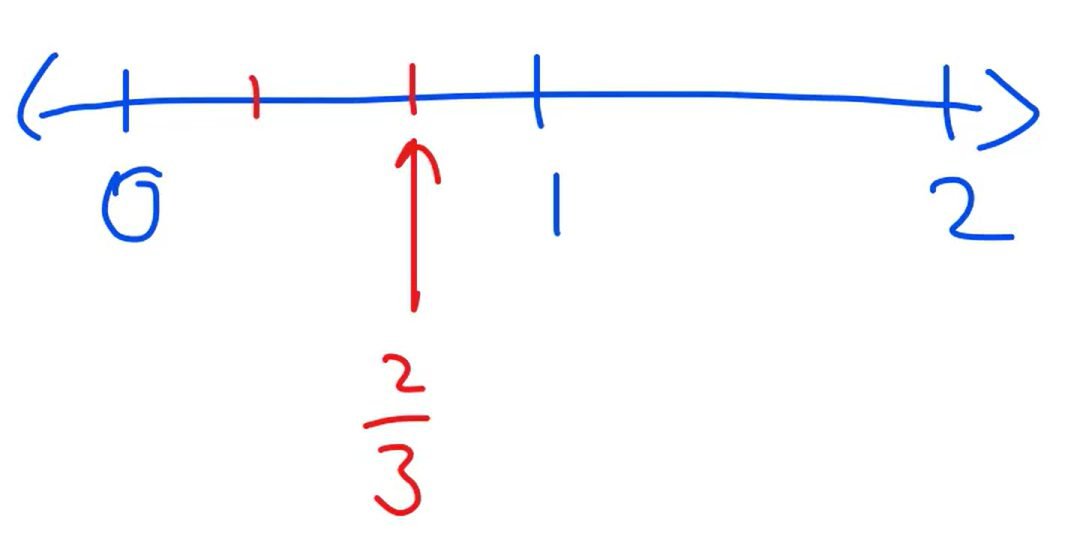
All the values given are relatively close to 1. When a value is less than 1, it is positioned between zero and 1. When it’s more than 1, it’s placed between 1 and 2.

Step 2: Position the given values.

The first value is $\frac{2}{3}$ , which means we split the area between zero and 1 into 3 equal parts.

number line

The second value is $\frac{4}{5}$ , meaning we have to cut the 0–1 interval into 5 equal parts

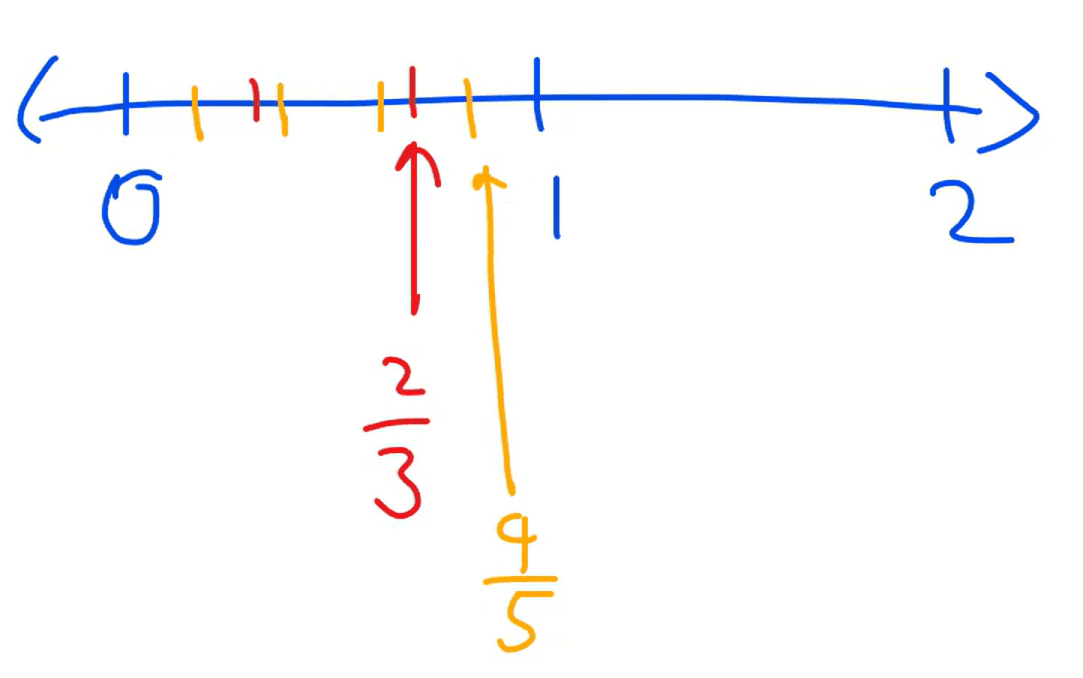
$fraction number line$

$\frac{4}{5}$ became closer to 1 than $\frac{2}{3}$ when we cut the number line proportionately as shown above.

1 $\frac{3}{4}$ lies between 1 and 2. So, we cut the number line into four parts as shown below.

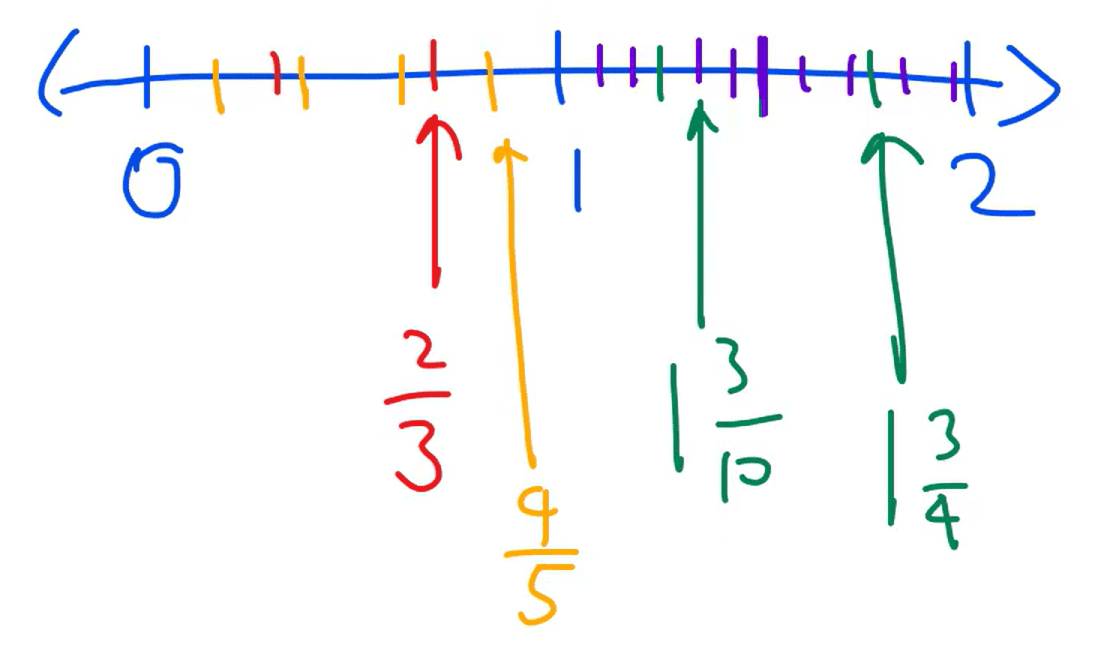
number line math

Step 3: Identify the value closest to 1.

The number line shows that the closest values to 1 are $\frac{4}{5}$ and $\frac{13}{10}$ .

How do we know which one is closer?

Well.. the key is to find the smaller the difference.

Important: The smaller the difference, the closer the fraction.

$\frac{4}{5}$ is $\frac{1}{5}$ away from 1. However, $\frac{13}{10}$ is $\frac{3}{10}$ away.

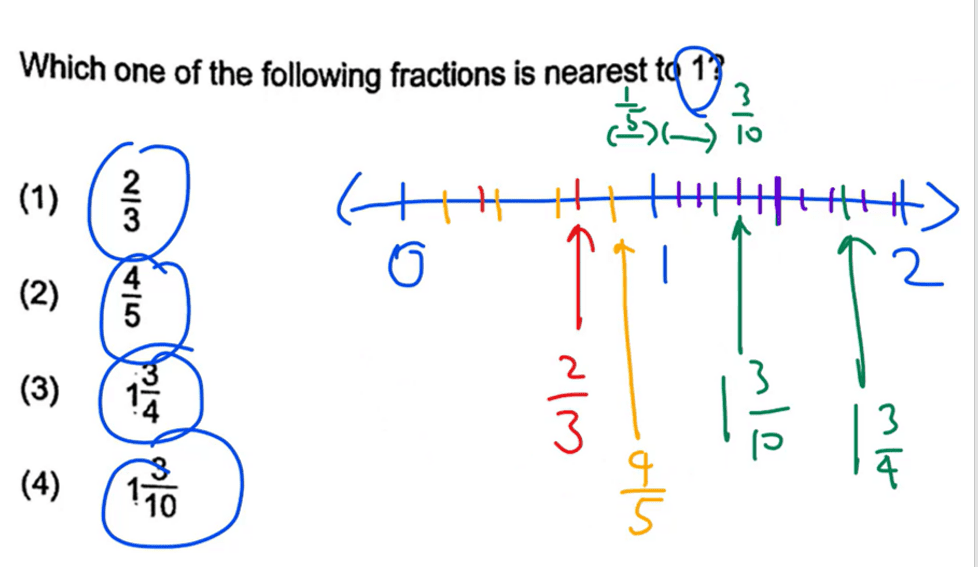
$which fraction is nearest psle math$

To compare $\frac{1}{5}$ and $\frac{3}{10}$ , we have to ensure that they have the same denominator. So, we multiply $\frac{1}{5}$ by 2 to get $\frac{2}{10}$ . So, $\frac{1}{5}$ = $\frac{2}{10}$ .

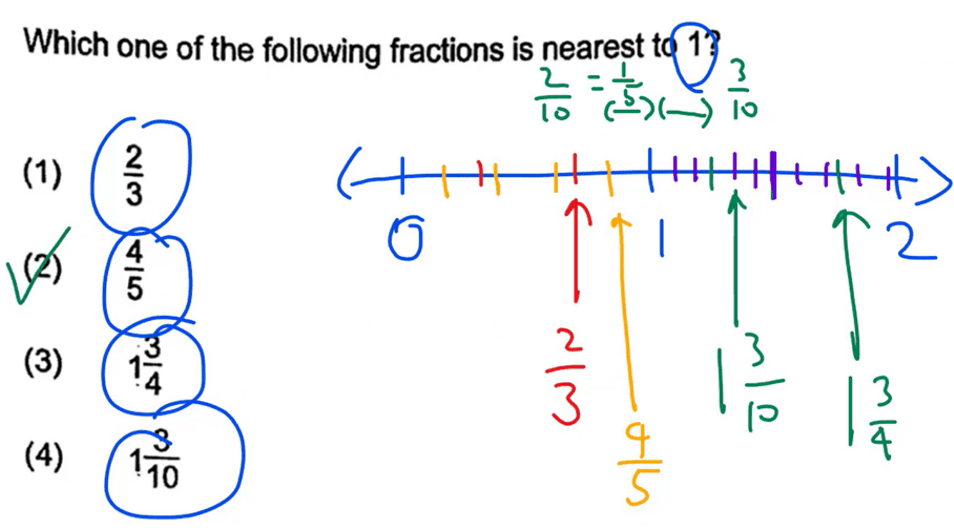
$which fraction is nearest psle math$

$\frac{2}{10}$ is smaller than $\frac{3}{10}$ , which means that $\frac{4}{5}$ is closer to 1.

Therefore, option (2) is the correct answer.

This question is relatively straightforward because we are just comparing the numerators.

The bigger the numerator, the bigger the entire value.

Example 2

The question was taken from the Henry Park Primary School 2022 P6 Prelim.

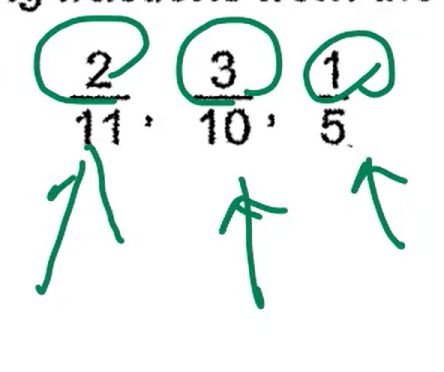
Question: Arrange the following fractions from the largest to the smallest.

Henry Park Primary School 2022 math prelims

We could make denominators the same and then compare the numerators.

However, the numbers in the denominators are pretty big, whereas the numerators are small.

Therefore, it will be easier to change the numerators to the same value.

The smallest common multiple for the numerators of $\frac{1}{5}$ is 6.

We can change the 3 fractions into the fractions below which have the same numerator of 6.

Now that we have common numerators, we can compare the denominator values.

Important: A bigger denominator value indicates that the entire value is smaller.

The smallest value will be $\frac{6}{33}$ and the largest will be $\frac{6}{20}$ , which is $\frac{3}{10}$ . The second largest value is then $\frac{6}{30}$ , which is $\frac{1}{5}$ .

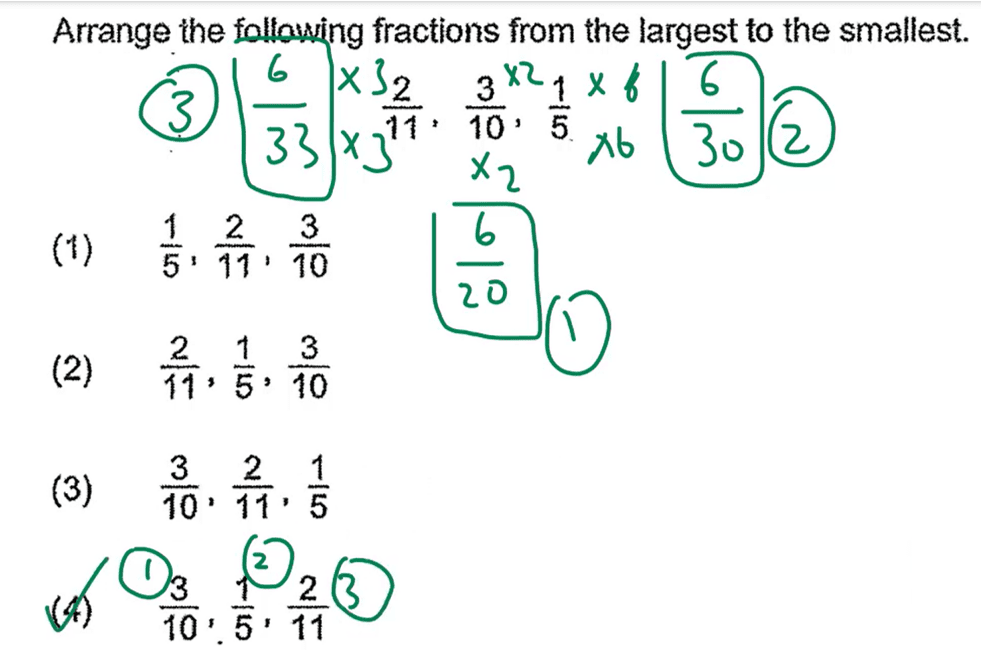
Henry Park Primary School 2022 math prelims

Therefore, the correct answer is Option 4.

Why is the fraction smaller when the denominator is bigger?

Let's say we have a pizza split among eight people ( $\frac{1}{8}$ ) and another split among four people ( $\frac{1}{4}$ ). The more people are sharing, the smaller the slice each person will receive. This means the entire value will be smaller.

Question:

The pie chart below shows the number of different coloured pens a bookshop sold. $\frac{1}{3}$ of the pens sold were green. $\frac{1}{4}$ of the pens sold were either purple or red and the rest were blue. What fraction of the pens sold were blue?

pie chart

Your child might be confused at first about the “either purple or red” pens in this question.

So, we can think of it as $\frac{1}{4}$ of the pens being both purple and red.

We can then write down that entire part as $\frac{1}{4}$ . The green is $\frac{1}{3}$ .

pie chart

Here, we have 1, $\frac{1}{3}$ and $\frac{1}{4}$ (1 - $\frac{1}{3}$ - $\frac{1}{4}$ ).

The common multiple is 12. So, $\frac{12}{12}$ - $\frac{4}{12}$ - $\frac{3}{12}$ = $\frac{5}{12}$

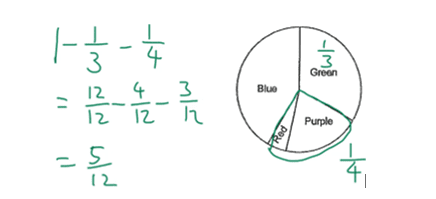
$pie chart fraction$

Therefore, the final answer is Option 2.

Example 4

This question was taken from the 2022 MGS P6 Prelim.

Question: There were $\frac{5}{7}$ as many red marbles as blue marbles in a jar. Dave took some blue marbles out of the jar and replaced them with the same number of red marbles. The number of red marbles became $\frac{5}{9}$ of all the marbles in the jar. Which of the following is a possible number of blue marbles that were replaced?

It is important to note that Dave did a replacement.

When there is a transfer of items, the total remains unchanged. (Constant Total Concept)

Your child will know that we can transform the fractions into a ratio.

Thus, red (R): blue (B) will be 5:7.

Similarly, we can transform the second fraction into R: total (T), which is 5:9.

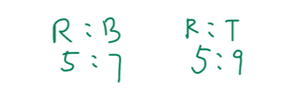
It is important to ask your child to identify the variable that did not change during the replacement process. The number of red and blue marbles changed, but the total did not change.

So, we get the total of the first ratio.

5 + 7 = 12.

Next, we determine the lowest common multiple of 12 and 9, which is 36.

We then change to total of both ratios to 36 as shown below.

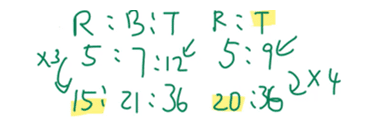
There were 15u red marbles before the replacement. It increased to 20u after replacement.

The increase of red marbles amounts to 5 units (5u).

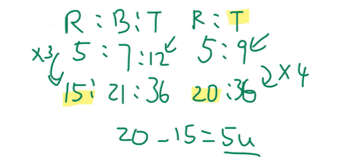
This 5u is also the number of blue marbles that were left in the jar.

Hence, that possible number is 5u and has to be a multiple of 5.

The only answer is Option 2 because the rest are not multiples of 5.

Example 5

Question: Joan, Siti and Xiuli had 60 beads each. Joan gave $\frac{2}{5}$ of her beads to Xiuli. Siti gave some of her beads to Xiuli. Xiuli had 3 times the total of the remaining beads Joan and Siti had. How many beads did Siti give to Xiuli?

In this process, there is a transfer wherein Joan and Siti are giving beads to Xiuli. So, your child will know that this kind of question deals with an internal transfer.

Internal transfer means that a friend is giving something to another friend. However, the total of the entire group does not change. (Constant Total Concept… Again!!)

As the total doesn’t change, we can find it first, which is 60 × 3 = 180.

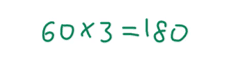
The total before and after the transfer is the same.

Here, Xiuli had 3 times the total of the remaining beads Joan and Siti had. That means that Xiuli (XL): Joan (J) + Siti (S) = 3:1 in the end. That means the total is 4 units (4u).

Therefore, 180/4 = 45. We can then find the number of beads Xiuli had, which is 45 × 3 = 135.

Xiuli received some beads from Joan, which is $\frac{2}{5}$ of the initial 60. So, we can go ahead and find $\frac{2}{5}$ of 60, which is 24.

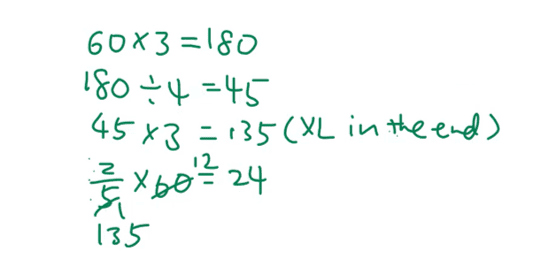
Xiuli received 24 beads from Joan.

We also know that Xiuli has 60 beads at first.

Now…

Can we find the number of beads which Siti give to Xiuli?

We simply take 135 – 24 – 60 = 51 (Ans)

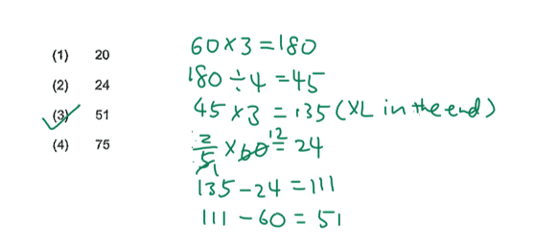
$mcqs on fractions$

Xiuli received 51 beads from Siti. Hence, option (3) is the correct answer.

I hope this tutorial was easy to understand, especially for your child in tackling MCQs on Fractions.

If you have any questions or suggestions for upcoming tutorials, feel free to leave a comment below and subscribe to our YouTube channel.

You can also watch the full video tutorial here:

Before you go, you might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.

This will be delivered to your email inbox.

Does your child need help in his or her studies?

1) Live Zoom Lessons at Grade Solution Learning Centre

math tuition class

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success. Here are the services we provide:

– Live Zoom lessons

– Adaptably™, an innovative smart learning platform featuring thousands of PSLE and exam-based questions tailored for your child’s practice. Adaptably not only tracks your child’s progress but also identifies their strengths and areas for improvement, providing valuable insights to enhance their learning journey.

– 24/7 Homework Helper Service

We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.

We specialise in English, Math, Science and Chinese subjects.

You can see our fees and schedules here >>

Primary Math Tuition

Secondary Math Tuition

2) Pre-recorded Online courses on Jimmymaths.com

psle math online course

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.

Your child can:

– Learn from recorded videos

– Get access to lots of common exam questions to ensure sufficient practice

– Get unlimited support and homework help

You can see the available courses here >> https://jimmymaths.digitrio.online/our-courses/