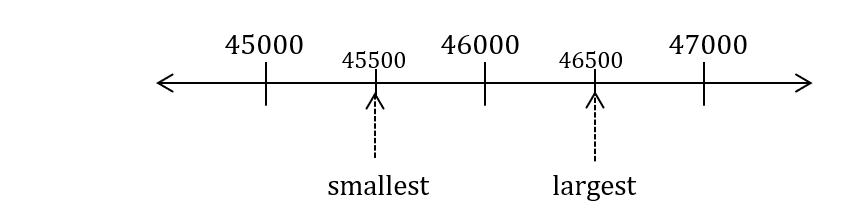
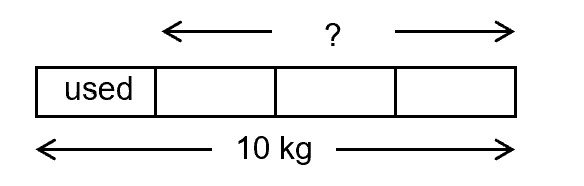
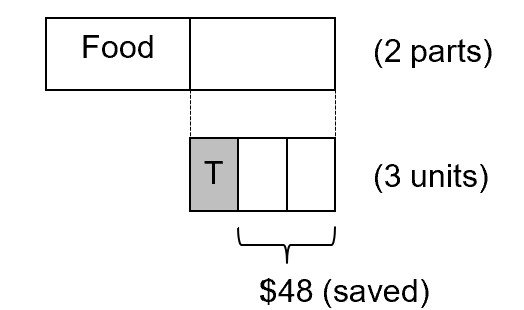
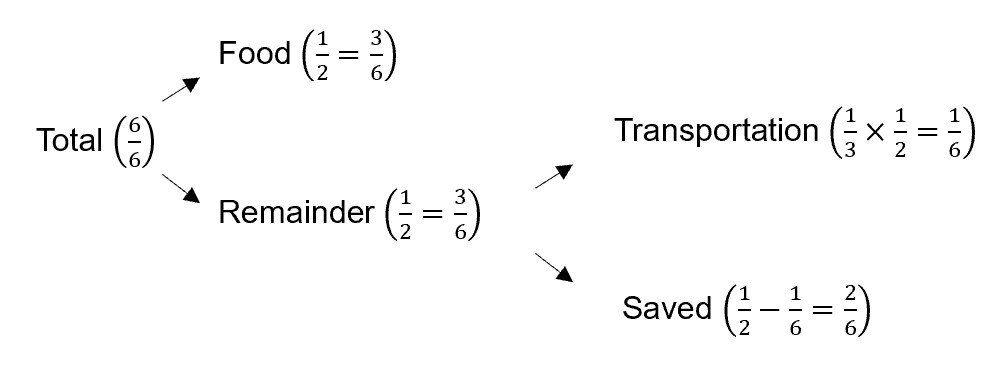
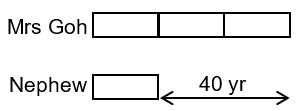
15 Common Types of P5 Math Questions
Struggling to figure out what types of Math questions your child needs to master in Primary 5?
You’re not alone. P5 is a crucial year where the jump in difficulty often catches students off guard, especially in problem sums.
In this article, we break down 15 common types of P5 Math questions that appear frequently in exams, so you’ll know exactly where to focus your child’s practice and build their confidence step by step.
Let’s dive in!