10 Most Common PSLE Math Problem Sums

Before you read on, you might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.

This will be delivered to your email inbox.

Remainder Concept

In general, there are 2 popular methods to solve problem sums involving “remainder”. They are using Model and Branching. In the example below, we will explore how to draw model and cut them to solve the question.

Example 1
John spent 3/5 of his money on books and 1/3 of the remainder on a wallet.
a) What fraction of his total money did he have left?
b) If John had $16 left, how much did he have at first?

Step 1: Draw a model and cut it into 5 units.

Step 2: Cut each unit into 3 units

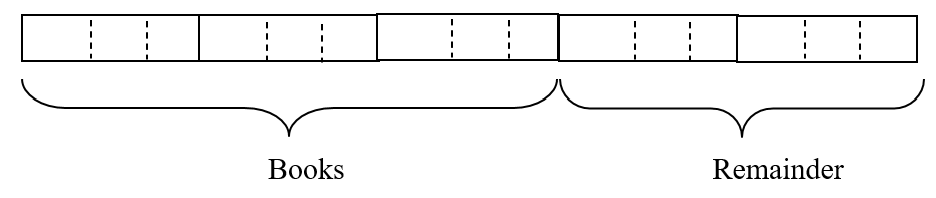
Step 3: Find the number of units for the wallet and leftover
Wallet → 1/3 ×6 = 2 units
Leftover → 6 – 2 = 4 units

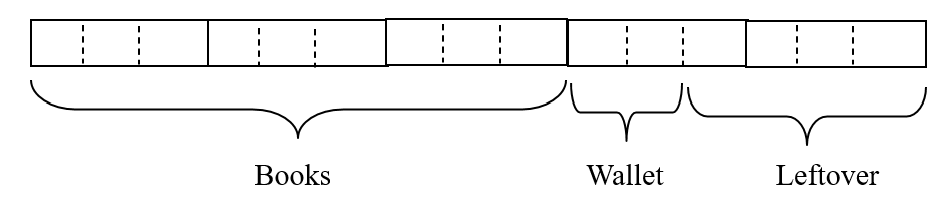
Step 4: Find the fraction that represent the leftover
4/15 (Ans for a)
Step 5: Find the amount he had at first.

4u = $16
1u = $4
15u = $60 (Ans for b)

Assumptions

Guess and Check method can be pretty time consuming. There is a faster and more systematic way which require you to make assumption or supposition. From your assumption, you then tweak it slightly and see the pattern. Let’s look at an example below:

Example 1

Miss Lee bought some sweets for her class of 15 students. Each girl received 5 sweets and each boy received 2 sweets. She bought a total of 57 sweets. How many boys were there in the class?

Step 1: Start with an assumption (If you want to find the number of boys, assume all are girls).
Assume there are 8 girls

Step 2: Find the total number of sweets
15 × 5 = 75

Step 3: Find the total difference in sweets (Big Difference)
75 – 57 = 18

Step 4: Find the difference in sweets between each boy and girl (Small Difference)
5 – 2 = 3

Step 5: Find the number of boys
18 ÷ 3 = 6 boys

Step 6: Check your answer!

Number of girls = 15 – 6 = 9
Total pencils = 9 × 5 + 6 × 2 = 57 (Correct)

Equal Fractions Concept

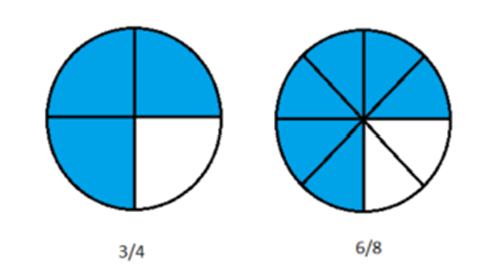
This is one of the most commonly tested problem sums which most students stumble. In this problem sum, you need to make the numerators equal (Not the denominator).

Example 1

87 people are dancing in a hall. of the male dancers is equal to
of the female dancers. How many more female dancers are there?

Step 1: Make the numerator the same

5/7 = 10/14

2/3 = 10/15

Step 2: Compare the denominator

Males : Females
= 14 : 15

Step 3: Find the total units
29u = 87

Step 4: Find 1 unit
1u = 3 (Answer)

More Than/Less Than

Questions with keywords “more than/less than” are commonly taught as “Before and After” questions by some teachers.

A good method to solve this type of questions is to draw models. Models give us a clear visualization of the “more than/less than” relationship. You need to be clear of cutting up models into equal parts.

Some students may find model drawing time confusing and troublesome. The alternative way is to use Algebra instead.

If you prefer to use Algebra, you need to be clear on how to solve equations using Algebraic methods.

We will use an example and solve it by the Model Drawing way.

Example 1 (Using Model Drawing)

Jenny had 150 more cupcakes than Denise. After Jenny gave away 1/5 of her cupcakes and Denise ate 3/4 of hers, Jenny had 208 more cupcakes than Denise. How many cupcakes did Denise have at first?

Step 1: Draw models for Jenny and Denise

Step 2: Change both fractions to the same denominator

1/5 = 4/20

3/4 = 15/20

Step 3: Cut both models into 20 units.

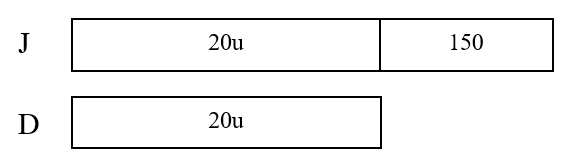
Step 4: Find the leftover portion for the ‘150’.

4/5 × 150 = 120

Step 5: Draw models for the leftovers.

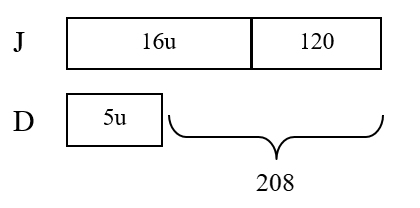
Step 6: Find 1 unit.

11u = 208 – 120
1u = 8
20u = 160 cupcakes (Answer)

Constant Part

Constant part concept are commonly tested in Ratio problem sums.

One part of the ratio changes while the other part remain constant. You need to identify the side which remain constant and make them to be the same.

You need to be familiar with the equal ratios concept.

Example 1

The ratio of the number of cars to the number of motorcycles in a carpark was 10 : 3. After 154 cars left the carpark, the ratio of the number of cars to that of motorcycles in the carpark became 3 : 2. How many cars remained in the car park?

At first

Cars : Motorcycles
= 10   :      3

After

Cars : Motorcycles
= 3     :      2

Since only cars left the carpark, the number of motorcycles remain the same before and after.

At first
Cars : Motorcycles
10    :      3
= 20    :      6

After
Cars : Motorcycles
= 3      :      2
= 20    :      6

Difference in units for the number of cars = 20 units – 9 units
= 11 units
11 units = 154
1 unit = 14
9 units = 126 cars

Constant Total

Constant Total means the total remained the same. Usually, this concept applies for question related to “Internal Transfer”.

If A transfer an amount to B, A will decrease while B will increase by the same amount. So the total will stay the same.

Example

Jia Wen had some stamps. The ratio of the number of local stamps to the number of foreign stamps owned by Jia Wen was 3 : 5. When Jia Wen gave away 65 local stamps and bought another 65 foreign stamps, the ratio became 2 : 5. How many stamps did Jia Wen have at first?

SOLUTION

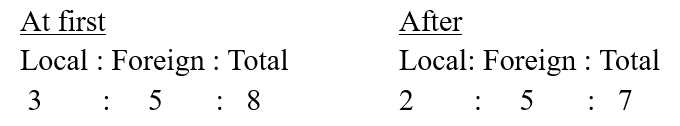
Since no. of local stamps and foreign stamps gave away and bought are equal, the number of total stamps before and after are the same.

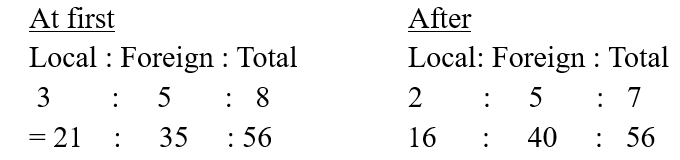
21 units – 16 units = 5 units
5 units = 65
1 unit = 13
56 units = 728 stamps

Constant Difference

Constant Difference means the difference remained the same. This happen when both quantities increase or decrease by the same amount.

Usually, this concept applies for problem sums related to “Age”.

As years go by, the age difference between 2 people will always be the same, because both will grow old together.

Example 1
The ages of Ali and Billy are in the ratio of 4 : 7. In 3 years’ time, their ages will be in the ratio of 3 : 5. How old is Billy now?

Step 1: Make the difference for Ali and Billy the same
Before:
A : B : Difference
= 4 : 7 : 3
= 8 : 14 : 6

After:
A : B : Difference
= 3 : 5 : 2
= 9 : 15 : 6

Step 2: Find the difference between Ali’s starting age and final age
9u – 8u = 1u

Step 3: Find 1 unit
1 unit = 3 years

Step 4: Find Billy’s age now
14 units = 42 years old (Ans)

Units and Parts

In this type of problem sums, nothing remained the same.

This type of Math problem sums are usually the last few 5 marks questions in the paper. So make sure you know how to do this type of questions.

Units and Parts involve using 2 letters, u and p, to represent 2 unknowns.

You can use the elimination method to solve for them.

Example 1

The ratio of Ali’s money to Billy’s money was 2 : 1. After Ali saved another $60 and Billy spent $150, the ratio became 4 : 1. How much money did Ali have at first?
Solutions:

Step 1: Write down the starting ratio and apply the changes.

Step 2: Compare the final units with the final ratio.
A : B
= 2u + 60 : 1u – 150
= 4 : 1

Step 3: Cross multiply the final units with the final ratio

Important Thought:

1 × (2u + 60) = 4 × (1u – 150)
2u + 60 = 4u – 600

Step 4: Solve for 1 unit

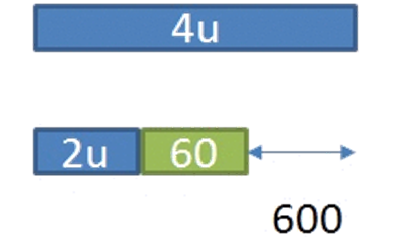
2 units = 60 + 600 = $660 (Ans)

Grouping Concept

The Grouping type of problem sums require you to group items together followed by finding the number of groups.

Example 1

Mark bought an equal number of shorts and shirts for $100. A shirt cost $8 and each pair of shorts cost $12. How much did he spend on the shirts?

Step 1: Group 1 shirt and 1 pair of shorts
8 + 12 = 20

Step 2: Find the number of groups
100 ÷ 20 = 5

Step 3: Find the amount spent on the shirts
5 × 8 = $40 (Ans)

Working Backwards

This is another common type of problem sums when you are given a final value, and you need to work backwards to find the starting value.

Example 1

A bus left an interchange carrying some passengers with it.
At the first stop, 1/4 of the people in it alighted and 5 people boarded it.
At the 2nd stop, 1/2 of the people in it alighted and 20 people boarded the bus.
When it left the 2nd stop, there were 60 passengers in it.
How many passengers were there in the bus when it left the interchange?

Step 1: Find the number of people before the 2nd stop
60 – 20 = 40
40 × 2 = 80

Step 2: Find the number of people before the 1st stop
80 – 5 = 75
75 ÷ 3 × 4 = 100 people (Ans)

Before you go, you might want to download this entire revision notes in PDF format to print it out for your child, or to read it later.

This will be delivered to your email inbox.

Click here to download

Does your child need help in his or her studies?

1) Live Zoom Lessons at Grade Solution Learning Centre

At Grade Solution Learning Centre, we are a team of dedicated educators whose mission is to guide your child to academic success.  Here are the services we provide:

– Live Zoom lessons

– Adaptably™, an innovative smart learning platform featuring thousands of PSLE and exam-based questions tailored for your child’s practice. Adaptably not only tracks your child’s progress but also identifies their strengths and areas for improvement, providing valuable insights to enhance their learning journey.

– 24/7 Homework Helper Service

We provide all these services above at a very affordable monthly fee to allow as many students as possible to access such learning opportunities.

We specialise in English, Math, Science and Chinese subjects.

You can see our fees and schedules here >>

Primary Math Tuition

Secondary Math Tuition

2) Pre-recorded Online courses on Jimmymaths.com

If you are looking for something that fits your budget, or prefer your child learn at his or her own pace, you can join our pre-recorded online Math courses.

Your child can:

– Learn from recorded videos

– Get access to lots of common exam questions to ensure sufficient practice

– Get unlimited support and homework help

You can see the available courses here >>

Math Online Courses